Одночлен і його стандартний вигляд — урок. Алгебра, 7 клас НУШ.

www.ua.pistacja.tv

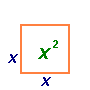
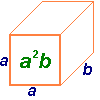
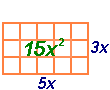
Вираз, що є добутком чисел, змінних та їх степенів називається одночленом.

Уже знайомі нам одночлени:


$x \cdot x = x^{2}$	$a \cdot a \cdot b = a^{2} b$	$3 x \cdot 5 x = (3 \cdot 5) \cdot (x \cdot x) = 15 x^{2}$

Вирази

6 \cdot a \cdot y

;

0,25 x^{3}

;

abbc

;

8,43

;

16 c \cdot (- \frac{1}{2}) d

;

\frac{3}{8} x^{2} y

також є одночленами.
При записі одночленів між числами та змінними знак множення не ставиться:

(

6 \cdot a \cdot y

$= 6ay$).

Одночленом також вважається:
— одна змінна, наприклад, $x$, бо

x = 1 \cdot x

;

— число, наприклад, $3$, бо

3 = 3 \cdot x^{0}

(одне число також є одночленом).

Зверни увагу!

Деякі одночлени можна спростити.

Спростимо одночлен

6 x y^{2} \cdot (- 2) x^{3} y

, використовуючи властивість множення степенів:

a^{m} \cdot a^{n} = a^{m + n}

6 x y^{2} \cdot (- 2) x^{3} y

6 \cdot (- 2) x x^{3} y^{2} y = - 12 x^{4} y^{3}

(числа перемножаються, а показники степенів з однаковими основами додаються).

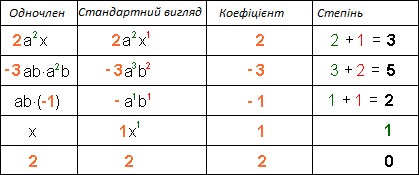
Стандартний вигляд одночлена

Якщо в одночлені першим записаний числовий множник, а добуток однакових степенів змінних записано у вигляді одного степеня, то такий вигляд одночлена називають стандартним виглядом.

Стандартним виглядом одночлена

10 \cdot \frac{1}{2} abbb

\frac{10 \cdot 1}{2} abbb = \frac{5 \cdot 2 \cdot 1}{2} a b^{3} = 5 a b^{3}

Зверни увагу!

Одночлен записаний у стандартному вигляді, якщо:
— добуток однакових змінних записано у вигляді степеня;
— числовий множник або коефіцієнт одночлена записаний першим множником в одночлені.

Одночлени 5; −9; $b$;

- b^{3}

— теж є одночленами стандартного вигляду.

Числовий множник одночлена, записаного у стандартному вигляді, називається коефіцієнтом одночлена.

(Коефіцієнти перемножуються між собою, змінні — між собою.)
Коефіцієнт одночлена

5 a b^{3}

дорівнює $5$, коефіцієнт одночлена

- 12 x^{4} y^{3}

дорівнює $–12$.

Коефіцієнти $1$ і $–1$ зазвичай не записуються.

1 a^{2} y = a^{2} y

- 1 x^{3} = - x^{3}

Степенем одночлена називається сума показників степенів усіх його змінних. Якщо одночлен не містить змінних (є числом), то вважається, що його степінь дорівнює нулеві.

Зверни увагу!

Для кожного одночлена можна вказати степінь.

Щоб визначити степінь одночлена, потрібно додати показники степенів усіх змінних (букв).

- 12 x^{4} y^{3}

— одночлен сьомого степеня ($4 + 3 = 7$);

$6a$ — одночленом першого степеня (змінна $a$ першого степеня);

$7$ — одночленом нульового степеня.

Подібні одночлени

Одночлени, у яких однакові буквені частини, тобто буквені частини є тотожно рівними виразами, називаються подібними одночленами.

Подібними одночленами є $3x^2y$ і $4x^2y$; $3bab$ і $2ab^2$; $6xy$ і $xy$; $5$ і $-3$.

Подібними одночленами не є $x^2y$ і $xy^2$.

Якщо в подібних одночленів рівні коефіцієнти, вони називаються рівними (однаковими) одночленами.

У цьому можна переконатися, записавши одночлени в стандартному вигляді.
З одночленів

8 x y^{3}; x y^{3}; 8 y^{3} x; 2 \cdot 4 xyyy; 8 x^{3} y

рівними є

8 x y^{3}; 8 y^{3} x; 2 \cdot 4 xyyy

У цьому можна переконатися, якщо записати всі одночлени в стандартному вигляді:

8 x y^{3}; x y^{3}; 8 y^{3} x; 2 \cdot 4 xyyy; 8 x^{3} y

$=>$

8 x y^{3}; x y^{3}; 8 {x y}^{3}; 8 {x y}^{3}; 8 x^{3} y

Якщо в подібних одночленів коефіцієнти є протилежними числами, одночлени називаються протилежними.

Серед одночленів

3 ac; - 9 ab; - 3 ac; abc; 9 ba

протилежними є

3 ac та - 3 ac; 9 ba та - 9 ba

Попередня тема

Повернутись до теми

Наступне завдання

Відправити відгук

Знайшли помилку?

Розкажіть нам!

1. Одночлен і його стандартний вигляд

Теорія: