Властивості квадратичної функції y=ax²

Графіком квадратичної функції

y = a x^{2} (a \neq 0)

є парабола, вершина якої знаходиться на початку координат.

Властивості квадратичної функції

y = {ax}^{2}

	$a > 0$ (Коефіцієнт $a$ додатний)	$a < 0$ (Коефіцієнт $a$ від'ємний)
Ескіз графіка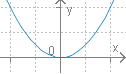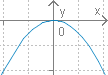
Розташування графіка	Вітки параболи спрямовані вгору.	Вітки параболи спрямовані вниз.
Інтервали зростання та спадання функції	Функція спадає, якщо $x \in (- \infty; 0]$ зростає, якщо $x \in [0; + \infty)$	Функція зростає, якщо $x \in (- \infty; 0]$ спадає, якщо $x \in [0; + \infty)$
Найбільше значення функції	Немає	$y = 0$
Найменше значення функції	$y = 0$	Немає
Інтервали, в яких значення функції додатне	Функція додатна ($y > 0$), якщо $x \in (- \infty; 0) \cup (0; + \infty)$ (графік знаходиться вище від осі $Ox$).	Немає
Інтервали, в яких значення функції від'ємне	Немає	Функція від'ємна ($y < 0$), якщо $x \in (- \infty; 0) \cup (0; + \infty)$ (графік знаходиться нижче від осі $Ox$).

Графік функції симетричний відносно осі $Oy$.

Якщо за умови зростання значень аргументу ($x$) зростають також значення функції ($y$), то функція є зростаючою.

Якщо за умови зростання значень аргументу ($x$) значення функції ($y$) убуває, то функція є спадною.

Чим більше модуль коефіцієнта $| a |$, тим ближче до осі $Oy$ знаходяться вітки параболи.

y = 5 x^{2}

y = \frac{1}{5} x^{2} або y = 0,2 x^{2}

Графіки квадратичної функції

y = {ax}^{2}

будуються за допомогою таблиці значень.

Приклад:

Маємо функцію

y = {3x}^{2}

. Обчисли значення функції, якщо аргумент дорівнює $1;-1;2;-2$.

$x$	$-2$	$-1$	$1$	$2$
$y$	$3 \cdot {(- 2)}^{2} = 3 \cdot 4 = \underline{12}$	$3 \cdot {(- 1)}^{2} = 3 \cdot 1 = \underline{3}$	$3 \cdot 1^{2} = 3 \cdot 1 = \underline{3}$	$3 \cdot 2^{2} = 3 \cdot 4 = \underline{12}$

Знайшли помилку?

\(x\)	\(-2\)	\(-1\)	\(1\)	\(2\)
\(y\)	$3 \cdot {(- 2)}^{2} = 3 \cdot 4 = \underline{12}$	$3 \cdot {(- 1)}^{2} = 3 \cdot 1 = \underline{3}$	$3 \cdot 1^{2} = 3 \cdot 1 = \underline{3}$	$3 \cdot 2^{2} = 3 \cdot 4 = \underline{12}$

5. Властивості квадратичної функції y=ax²