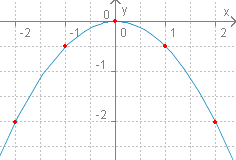
Побудова графіка квадратичної функції за умови, що \(a < 0\)
Якщо \(a\) від'ємне (\(a < 0\)), то вітки параболи спрямовані вниз.
1. Вершина параболи знаходиться на початку координат.
2. Замість аргументу (\(x\)) підставляються два додатних і два від'ємних значення, наприклад, \(1; 2 \) і \(- 1; -2\). Знаходяться значення функції (\(y\)) в цих точках.
3. Отримані точки позначаються на координатній площині та з'єднуються лінією.
2. Замість аргументу (\(x\)) підставляються два додатних і два від'ємних значення, наприклад, \(1; 2 \) і \(- 1; -2\). Знаходяться значення функції (\(y\)) в цих точках.
3. Отримані точки позначаються на координатній площині та з'єднуються лінією.
Зверни увагу!
При обчисленні значень функції спочатку виконується піднесення до степеня, а потім множення.
Приклад:
Побудуй графік функції .
\(x\)
| \(y\)
| Обчислення |
\(2\)
| \(-2\)
| |
\(1\)
| \(-0,5\)
| |
\(0\)
| \(0\)
| |
\(-1\)
| \(-0,5\)
| |
\(-2\)
| \(2\)
|