Зручно при розв'язанні квадратних нерівностей використовувати метод інтервалів.
Розглянемо етапи методу інтервалів:
- знаходять корені квадратного тричлена і розкладають на множники;
- відзначають на числовій прямій корені тричлена і знаходять знаки квадратного тричлена на кожному інтервалі;
- обирають інтервал, відповідний знаку нерівності і записують відповідь.
- знаходять корені квадратного тричлена і розкладають на множники;
- відзначають на числовій прямій корені тричлена і знаходять знаки квадратного тричлена на кожному інтервалі;
- обирають інтервал, відповідний знаку нерівності і записують відповідь.
Приклад:
Розв'язати нерівність.
Розв'язання. Знайдемо корені квадратного тричлена
і розкладемо його на множники за формулою
Зазначимо на числовій прямій корені і знайдемо знаки квадратного тричлена на кожному інтервалі.
Для цього з кожного інтервалу достатньо взяти по одному значенню і підставити замість \(x\) у тричлен.
Для цього з кожного інтервалу достатньо взяти по одному значенню і підставити замість \(x\) у тричлен.
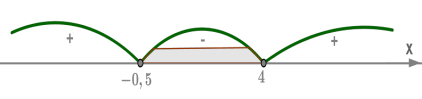
На інтервалі візьмемо \(x=-2\), тоді
На інтервалі візьмемо \(x=0\), тоді
На інтервалі візьмемо \(x=5\), тоді
Квадратний тричлен приймає від'ємні і рівні нулю значення на інтервалі .
Відповідь: