Знаки нерівностей — урок. Алгебра, 9 клас.

Нерівності, добуток або частка яких зрівняно з нулем, це, наприклад,

(x + 3) (x - 2) > 0; \frac{x + 3}{x - 5} \leq 0

Один з методів розв'язання таких нерівностей — заміна системою нерівностей.

Щоб замінити нерівність системами нерівностей, потрібно знати властивості знаків:

\begin{array}{l} (+) (+) = (+) (-) (-) = (+) (+) (-) = (-) (-) (+) = (-) \\ \frac{(+)}{(+)} = (+) \frac{(-)}{(-)} = (+) \frac{(+)}{(-)} = (-) \frac{(-)}{(+)} = (-) \end{array}

Щоб добуток був додатним, обидва множники повинні мати однакові знаки - або додатні, або від'ємні.

Щоб добуток був від'ємним, множники повинні мати протилежні знаки.

\begin{array}{l} f (x) \cdot g (x) > 0 тільки в тому випадку, якщо \{\begin{cases} f (x) > 0 \\ g (x) > 0 \end{cases} або \{\begin{cases} f (x) < 0 \\ g (x) < 0 \end{cases} \\ f (x) \cdot g (x) < 0 тільки в тому випадку, якщо \{\begin{cases} f (x) > 0 \\ g (x) < 0 \end{cases} або \{\begin{cases} f (x) < 0 \\ g (x) > 0 \end{cases} \\ f (x) \cdot g (x) \geq 0 тільки в тому випадку, якщо \{\begin{cases} f (x) \geq 0 \\ g (x) \geq 0 \end{cases} або \{\begin{cases} f (x) \leq 0 \\ g (x) \leq 0 \end{cases} \\ f (x) \cdot g (x) \leq 0 тільки в тому випадку, якщо \{\begin{cases} f (x) \geq 0 \\ g (x) \leq 0 \end{cases} або \{\begin{cases} f (x) \leq 0 \\ g (x) \geq 0 \end{cases} \end{array}

Щоб частка була додатною, ділене і дільник повинні мати однакові знаки.

Щоб частка була від'ємною, ділене і дільник повинні мати протилежні знаки.

\begin{array}{l} \frac{f (x)}{g (x)} > 0 тільки в тому випадку, якщо \{\begin{cases} f (x) > 0 \\ g (x) > 0 \end{cases} або \{\begin{cases} f (x) < 0 \\ g (x) < 0 \end{cases} \\ \frac{f (x)}{g (x)} < 0 тільки в тому випадку, якщо \{\begin{cases} f (x) > 0 \\ g (x) < 0 \end{cases} або \{\begin{cases} f (x) < 0 \\ g (x) > 0 \end{cases} \\ \frac{f (x)}{g (x)} \geq 0 тільки в тому випадку, якщо \{\begin{cases} f (x) \geq 0 \\ g (x) > 0 \end{cases} або \{\begin{cases} f (x) \leq 0 \\ g (x) < 0 \end{cases} \\ \frac{f (x)}{g (x)} \leq 0 тільки в тому випадку, якщо \{\begin{cases} f (x) \geq 0 \\ g (x) < 0 \end{cases} або \{\begin{cases} f (x) \leq 0 \\ g (x) > 0 \end{cases} \end{array}

Зверни увагу!

Зверни увагу - в дробовій нерівності знаменник не може дорівнювати \(0\), тому використовуються тільки знаки строгої нерівності (\(<\) або \(>\)).

Приклад:

\begin{array}{l} \frac{x + 2}{x - 3} \geq 0 \\ \{\begin{cases} x + 2 \geq 0 \\ x - 3 > 0, оскільки x + 3 \neq 0 \end{cases} або \{\begin{cases} x + 2 \leq 0 \\ x - 3 < 0 \end{cases} \\ \{\begin{cases} x \geq - 2 \\ x > 3 \end{cases} (1) або \{\begin{cases} x \leq - 2 \\ x < 3 \end{cases} (2) \end{array}

Множини розв'язків системи нерівностей відображаються на осі координат:

(1)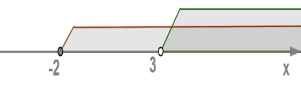
(2)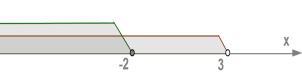

Відповідь:

x \in (- \infty; - 2] \cup (3; + \infty)

Знайшли помилку?

2. Знаки нерівностей