Перший спосіб.
Будують графік функції і знаходять точки його перетину з віссю \(x\).
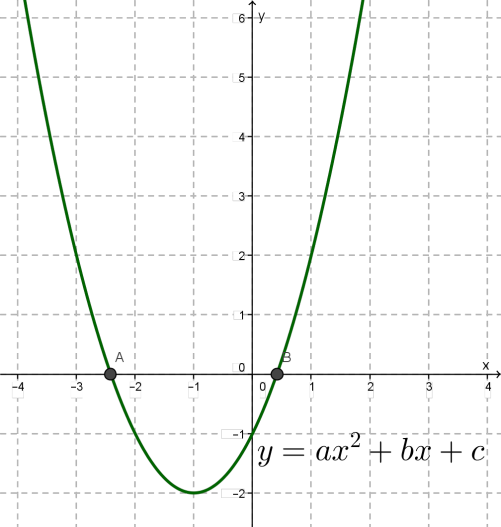
Другий спосіб.
Перетворюють рівняння до вигляду , будують параболу і пряму \(y = -bx - c\), знаходять точки їх перетину (коренями рівняння є абсциси точок перетину, якщо такі є).
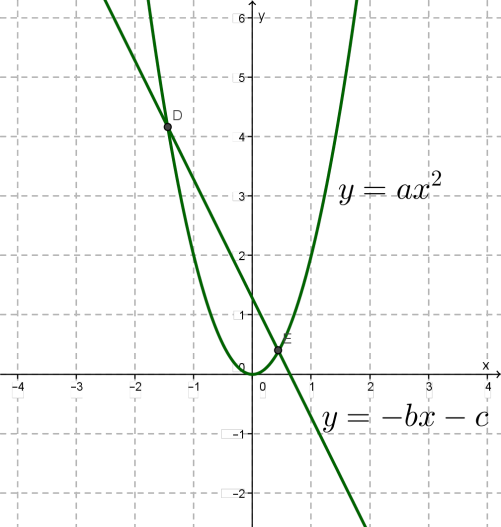
Третій спосіб.
Перетворюють рівняння до виду , будують параболу і пряму \(y = -bx\) (вона проходить через початок координат); знаходять точки їх перетину.
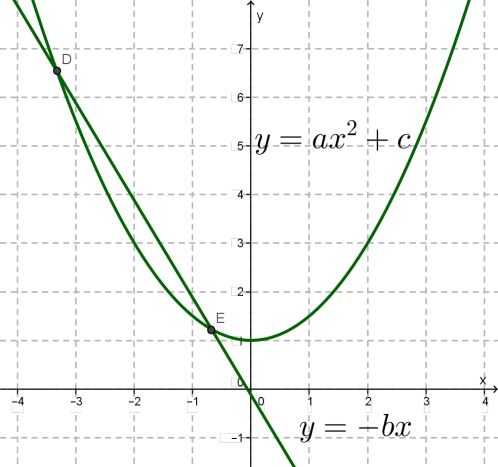
Четвертий спосіб.
Застосовуючи метод виділення повного квадрата, перетворюють рівняння до вигляду Будують параболу і пряму \(y = - m\), паралельну осі \(x\); знаходять точки перетину параболи і прямої.
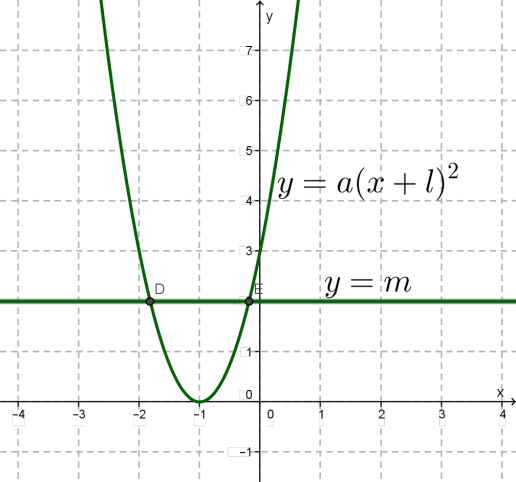
П'ятий спосіб.
Зводять рівняння до вигляду , тобто далі .Будують гіперболу (це гіпербола за умови, що ) і пряму \(y = - ax - b\); знаходять точки їх перетину.
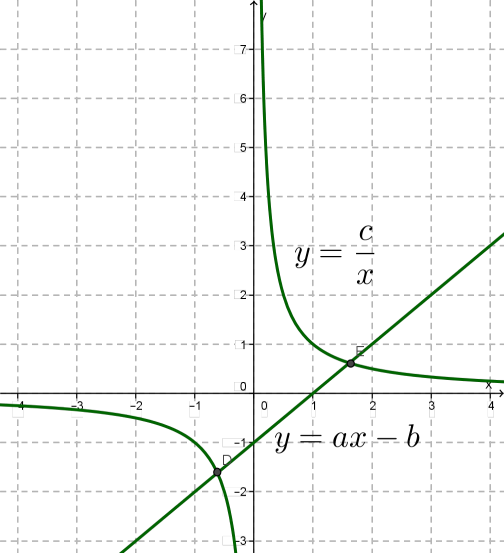
Зауважимо, що перші чотири способи застосовуються до будь-яких рівнянь вигляду, а п'ятий — тільки до тих, у яких . На практиці можна вибирати той спосіб, який тобі здається найбільш раціональним до даного рівняння, або, який тобі більше подобається (або більш зрозумілий).
Незважаючи на велику кількість способів графічного розв'язання квадратних рівнянь, впевненості в тому, що будь-яке квадратне рівняння ми зможемо розв'язати графічно, немає. Нехай, наприклад, потрібно розв'язати рівняння (спеціально візьмемо рівняння, схоже на те, що було в розглянутому прикладі). Спробуємо його розв'язати, наприклад, другим способом: зведемо рівняння до вигляду , побудуємо параболу і пряму \(y = x + 3\).
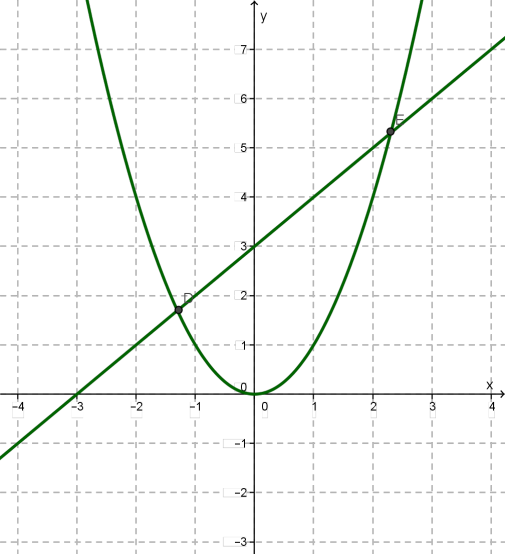
Вони перетинаються в точках \(D\) та \(E\), отже, рівняння має два кореня. Але чому дорівнюють ці корені, ми за допомогою креслення сказати не можемо — точки \(D\) та \(E\) мають не такі «хороші» координати.
А тепер розглянемо рівняння . Спробуємо його розв'язати, скажімо, третім способом. Зведено рівняння до вигляду . Тут треба побудувати параболу і пряму \(y = 16x\). Але обмежені розміри аркуша зошита не дозволяють цього зробити, адже параболу треба опустити на \(95\) клітин вниз.
Таким чином, графічні способи розв'язання квадратного рівняння красиві і приємні, але не дають стовідсоткової гарантії розв'язання будь-якого квадратного рівняння. Врахуємо це надалі.
