Квадратні нерівності — урок. Алгебра, 9 клас.

Загальний вигляд квадратних нерівностей, це

a x^{2} + bx + c > 0 (< 0, \leq 0, \geq 0), де a \neq 0

Множину розв'язків квадратної нерівності легко визначити, приблизно накресливши графік функції

y = a x^{2} + bx + c

(параболу).

Кроки розв'язання квадратної нерівності:

1. Визначаються точки перетину параболи і осі $x$ за допомогою розв'язання рівняння

a x^{2} + bx + c = 0

Згадаємо формули коренів квадратного рівняння:

$\begin{array}{l} D = b^{2} - 4 ac \\ x_{1} = \frac{- b + \sqrt{D}}{2 a}, x_{2} = \frac{- b - \sqrt{D}}{2 a} \end{array}$

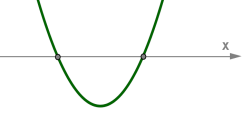
Якщо $D > 0$, у рівняння два різних кореня, парабола перетинає вісь $x$ у двох точках
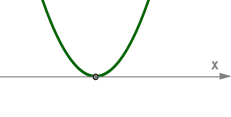
Якщо $D = 0$, у рівняння два однакових кореня, вершина параболи знаходиться на осі $x$
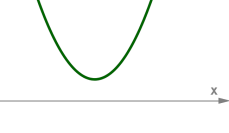
Якщо $D < 0$, у рівняння немає коренів, парабола не перетинає вісь $x$

2. Враховуючи кількість коренів і знак коефіцієнта $a$, креслиться графік параболи.

Зверни увагу!

Якщо $a > 0$, гілки параболи спрямовані вгору, якщо $a < 0$, тоді вниз.

Порада: якщо хочеш, щоб гілки параболи завжди були спрямовані вгору, у випадках, коли $a<0$, треба спочатку обидві частини нерівності помножити на ($-1$). Не забудь, що на протилежний поміняється знак нерівності.

3. Обираються порожні або зафарбовані точки, в залежності від вигляду знака нерівності: