Нерівності виду \(a>b\) і \(c>d\) або \(a<b\) і \(c<d\), (тобто нерівності з однаковими знаками) називають нерівностями однакового змісту.
Нерівності виду \(a>b\) і \(c<d\) або \(a<b\) і \(c>d\), (тобто нерівності з різними, протилежними знаками) називають нерівностями протилежного змісту.
Приклад:
Нерівності \(x>-5\) і \(y>17\) є нерівностями однакового змісту,
а нерівності \(х<-5\) і \(y>17\) нерівностями протилежного змісту
а нерівності \(х<-5\) і \(y>17\) нерівностями протилежного змісту
Зверни увагу!
Якщо одночасно виконуються дві умови \(x>a\) () та \(x<b\) (),
тоді можна записати замість двох нерівностей одну подвійну нерівність \(a<x<b\).
Множину всіх значень змінної \(x\) подвійної нерівності \(a<x<b\) можна зобразити на числовій прямій.
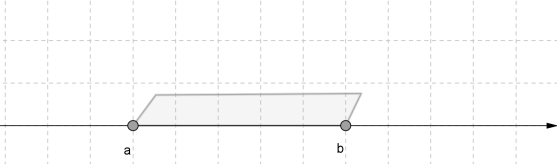
Зверни увагу!
Подвійна нерівність читається з середини: \(x\) більше \(a\), але менше \(b\).
читається, як \(x\) більше \(47,2\), але менше \(47,3\).
