Властивість 1. Якщо \(a>b\) і \(b>c\), тоді \(a>c\).
Це можна зобразити на числовій прямій.
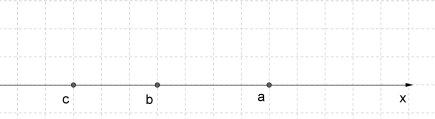
Перевіримо на прикладі.
Нехай \(a=6, b=0, c=-4\), тоді, якщо \(6>0\) і \(0>-4\), тоді \(6>-4\).
Властивість 2. Якщо \(a>b\), тоді \(a+c>b+c\).
Якщо до обох частин нерівності додати одне й те саме число - знак нерівності не зміниться.
Властивість 3. Якщо \(a>b\) і \(k>0\), тоді \(ak>bk\).
Якщо обидві частини нерівності помножити на одне і те ж додатне число - знак нерівності не зміниться
Приклад:
Відомо, що \(17,2 < x < 17,3\). Оцінити \(2x\).
При множенні подвійної нерівності на додатне число \(2\),
отримаємо нерівність того ж змісту (тобто знаки не зміняться).
отримаємо нерівність того ж змісту (тобто знаки не зміняться).
Властивість 4. Якщо \(a>b\) і \(k<0\), тоді \(ak<bk\).
Якщо обидві частини нерівності помножити на одне і те ж від'ємне число - знак нерівності зміниться ( \(< \) на \(>\), \(>\) на \(< \))
Приклад:
Відомо, що \(17,2 < x < 17,3\). Оцінити \(-2x\).
При множенні подвійної нерівності на від'ємне число \(-2\),
отримаємо нерівність протилежного змісту (тобто знаки зміняться).
отримаємо нерівність протилежного змісту (тобто знаки зміняться).
Зверни увагу!
Ділення на число \(k\) можна замінити множенням на дріб