Наслідки з аксіом
1. Через пряму і точку, що не лежить на ній, можна провести площину, при тому тільки одну.
Доведення:
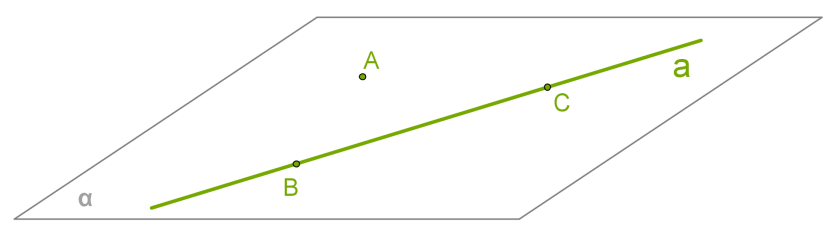
1) Розглянемо пряму \(a\) і точку \(A\), яка не знаходиться на цій прямій.
2) На прямій \(a\) оберемо точки \(B\) і \(C\).
3) Оскільки всі три точки не лежать на одній прямій, з другої аксіоми випливає, що через точки \(A\), \(B\), \(C\) і можна провести одну єдину площину .
4) Точки прямої \(a\), \(B\) і \(C\), лежать на площині , тому з третьої аксіоми випливає, що площина проходить через пряму \(a\) і, звичайно, через точку \(A\).
1) Розглянемо пряму \(a\) і точку \(A\), яка не знаходиться на цій прямій.
2) На прямій \(a\) оберемо точки \(B\) і \(C\).
3) Оскільки всі три точки не лежать на одній прямій, з другої аксіоми випливає, що через точки \(A\), \(B\), \(C\) і можна провести одну єдину площину .
4) Точки прямої \(a\), \(B\) і \(C\), лежать на площині , тому з третьої аксіоми випливає, що площина проходить через пряму \(a\) і, звичайно, через точку \(A\).
2. Через дві прямі, що перетинаються, можна провести площину, притому тільки одну.
Доведення:
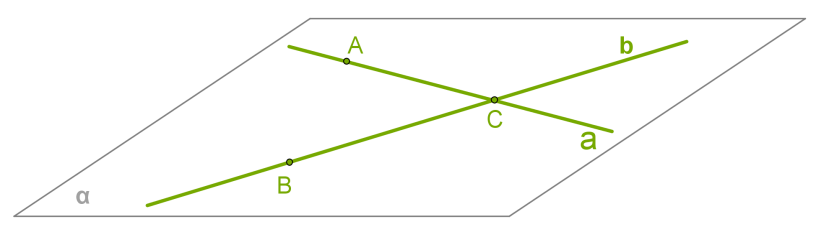
1) Розглянемо прямі \(a\) і \(b\), які перетинаються в точці \(C\).
2) Оберемо точку \(A\) на прямій \(a\) і точку \(B\) на прямій \(b\) так, щоб ці точки не збігалися з точкою \(C\).
3) З другої аксіоми випливає, що через точки \(A\), \(B\) і \(C\) можна провести одну єдину площину . У такому випадку прямі \(a\) і \(b\) знаходяться на площині (з третьої аксіоми).
1) Розглянемо прямі \(a\) і \(b\), які перетинаються в точці \(C\).
2) Оберемо точку \(A\) на прямій \(a\) і точку \(B\) на прямій \(b\) так, щоб ці точки не збігалися з точкою \(C\).
3) З другої аксіоми випливає, що через точки \(A\), \(B\) і \(C\) можна провести одну єдину площину . У такому випадку прямі \(a\) і \(b\) знаходяться на площині (з третьої аксіоми).
Приклад:
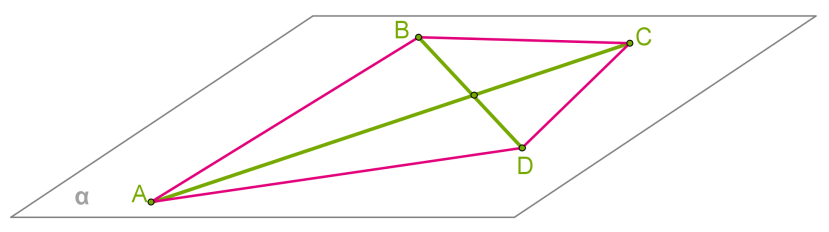
Дано відрізки, що перетинаються, \(AC\) і \(BD\). Довести, що всі відрізки \(AB\), \(BC\), \(CD\), \(DA\) знаходяться на одній площині.
Розв'язання:
1) З другої теореми випливає, що через \(AC\) і \(BD\) можна провести тільки одну площину, яку позначимо . Це означає, що точки \(A, B, C\) і \(D\) належать площині .
2) З третьої аксіоми випливає, що всі точки прямих \(AB\), \(BC\), \(CD\) і \(DA\) належать площині. Тому всі відповідні відрізки лежать на площині .
2) З третьої аксіоми випливає, що всі точки прямих \(AB\), \(BC\), \(CD\) і \(DA\) належать площині. Тому всі відповідні відрізки лежать на площині .
