Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, що з'єднує дану точку з точкою площини, який не є перпендикуляром до площини.
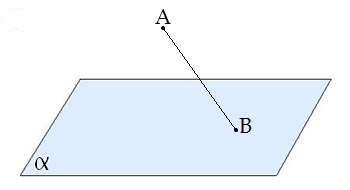
\(AB\) — похила.
\(B\) — основа похилої.
\(B\) — основа похилої.
Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що з'єднує дану точку з точкою площини і лежить на прямій, перпендикулярній площині.
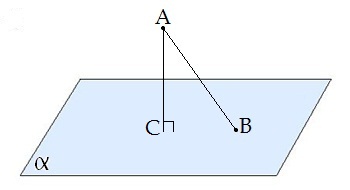
\(AC\) — перпендикуляр.
\(C\) — основа перпендикуляра.
Відстанню від точки до площини називається довжина перпендикуляра, проведеного з цієї точки до площини.
Відрізок, що з'єднує основи перпендикуляра і похилої, проведених з однієї і тієї ж точки, називається проекцією похилої.
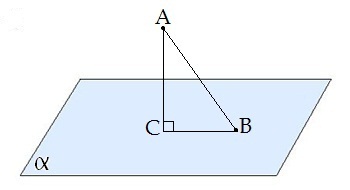
\(CB\) — проекця похилої \(AB\) на площину .
Трикутник \(ABC\) прямокутний.
Кутом між похилою і площиною називається кут між цією похилою і її проекцією на площину.
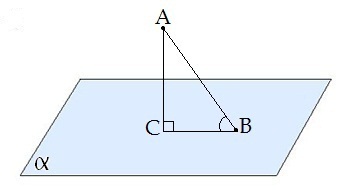
\(CBA\) — кут між похилою \(AB\) і площиною .
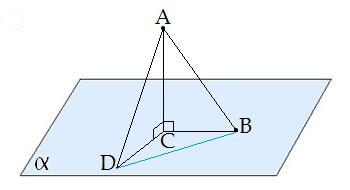
Якщо \(AD > AB\), то \(DC > BC\).
Якщо з даної точки до даної площини провести кілька похилих, то більшій похилій відповідає більша проекція.
\(DAB\) — кут між похилими,
\(DCB\) — кут між проекціями.
Відрізок \(DB\) — відстань між основами похилих.