Піраміда, основою якої є правильний багатокутник, а вершина якої проектується в центр основи, називається правильною пірамідою.
Бічні грані правильної піраміди — рівні трикутники.
Висота бічної грані правильної піраміди називається апофемою.
Висота бічної грані правильної піраміди називається апофемою.
Правильна трикутна піраміда, у якої всі ребра рівні, називається тетраедром.
Всі грані тетраедра — рівні рівносторонні трикутники.
Всі грані тетраедра — рівні рівносторонні трикутники.
У середній школі потрібно вміти розв'язувати задачі, де задана
- правильна трикутна піраміда;
- правильна чотирикутна піраміда;
- правильна шестикутна піраміда.
- правильна трикутна піраміда;
- правильна чотирикутна піраміда;
- правильна шестикутна піраміда.
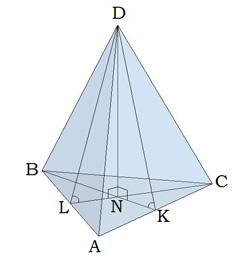
Правильна трикутна піраміда
Основа правильної трикутної піраміди — рівносторонній трикутник.
Вершина піраміди проектується в точку перетину медіан.
Запам'ятай:
Вершина піраміди проектується в точку перетину медіан.
Запам'ятай:
\(BN:NK = 2:1\)
\(KD\) — апофема,
\(NKD\) і \(NLD\) — двогранні кути при основі піраміди,
\(DCN\) і \(DBN\) — кути між бічним ребром і площиною основи піраміди.
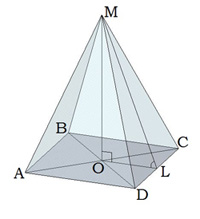
Правильна чотирикутна піраміда
Основа правильної чотирикутної піраміди — квадрат.
Вершина піраміди проектується в точку перетину діагоналей основи (квадрата).
Вершина піраміди проектується в точку перетину діагоналей основи (квадрата).
\(ML\) — апофема,
\(MLO\) — двогранний кут при основі піраміди,
\(MCO\) — кут між бічним ребром і площиною основи піраміди.
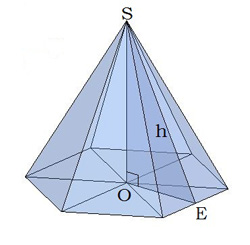
Правильна шестикутна піраміда
Основа правильної шестикутної піраміди — правильний шестикутник.
Вершина піраміди проектується в точку перетину діагоналей основи (шестикутника).
Вершина піраміди проектується в точку перетину діагоналей основи (шестикутника).
\(SE = h\) — апофема,
\(OES\) — двогранний кут при основі піраміди.
Формули.
Для обчислення площі бічної поверхні правильної піраміди існують дві формули:
, де \(P\) — периметр основи, \(h\) — апофема, — двогранний кут при основі.
Об'єм піраміди \(V =\) , де \(H\) — висота піраміди.
Зверни увагу!
Не плутай \(h\) — апофему з \(H\) — висотою піраміди!
