Якщо бічні грані піраміди з її основою утворюють рівні двогранні кути, тоді всі висоти бічних граней піраміди рівні (у правильної піраміди це апофеми), вершина піраміди проектується в центр кола, вписаного в багатокутник основи.
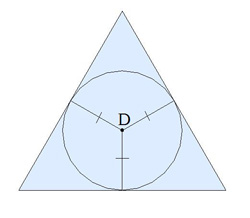
Щоб легше це запам'ятати, можна уявити, що ви бачите піраміду зверху.
Проекції висот бічних граней піраміди рівні, через їх кінці можна вписати коло.
Проекції висот бічних граней піраміди рівні, через їх кінці можна вписати коло.
Для таких пірамід при обчисленні площі бічної поверхні застосовуються формули, які використовуються для правильної піраміди.
де \(h\) — висота бічної грані, — двогранний кут
У піраміди можуть бути рівні двогранні кути при основі тоді, коли в багатокутник основи можна вписати коло.
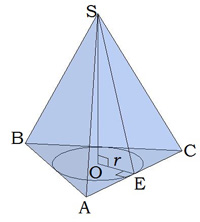
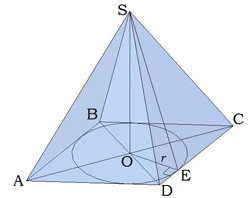
Зверни увагу!
Позначаючи радіус \(r\) на малюнку, потрібно бути дуже уважним! Радіус вписаного кола перпендикулярний стороні.
Наприклад, в довільному трикутнику він не перебуває на бісектрисі і в ромбі не паралельний стороні.
Головні залежності для багатокутників, в які можна вписати коло
| Багатокутник | Центр вписаного кола | Формули |
будь-який трикутник | точка перетину бісектрис | , де \(p\) — півпериметр |
ромб | точка перетину діагоналей |
