Формула діагоналі прямокутного паралелепіпеда

Пряма призма, основою якої є прямокутник, називається прямокутним паралелепіпедом.

Довжини трьох ребер, що мають спільну вершину, називаються вимірами прямокутного паралелепіпеда.

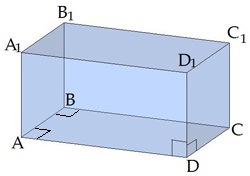
Наприклад, три виміри — це довжини трьох ребер

{DA, DC, DD}_{1}

Квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів:

D^{2} = a^{2} + b^{2} + c^{2}

де \(a, b, c\) — виміри прямокутного паралелепіпеда, тобто, його довжина, ширина і висота.

На малюнку:

{D B_{1}}^{2} = {DA}^{2} + {DC}^{2} + {D D_{1}}^{2}

Зверни увагу!

У прямокутного паралелепіпеда всі діагоналі рівні:

D B_{1} = C A_{1} = A C_{1} = B D_{1}

Приклад:

Формула діагоналей куба

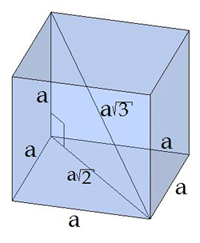
Оскільки у куба всі виміри рівні, позначаємо їх за \(a\), тоді

D^{2} = a^{2} + a^{2} + a^{2} = 3 a^{2}

Спрощуємо і отримуємо формулу діагоналі куба:

D = a \sqrt{3}

Знайшли помилку?

4. Формула діагоналі прямокутного паралелепіпеда