Куля та сфера

Сферична поверхня (сфера) — це геометричне місце точок (тобто безліч всіх точок) в просторі, рівновіддалених від однієї даної точки, яка називається центром сферичної поверхні (сфери).
На малюнку всі точки рівновіддалені від точки \(C\), радіус \(CA\) з'єднує центр з точкою на сфері.
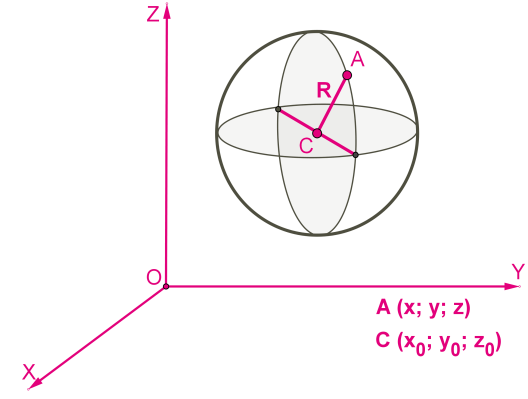
Всі відстані від центра до будь-якої точки на сфері однакові й дорівнюють радіусу. Використовуючи формулу відстані між точками з даними координатами, можна отримати рівняння сфери:
Куля — це тіло, обмежене сферичною поверхнею.
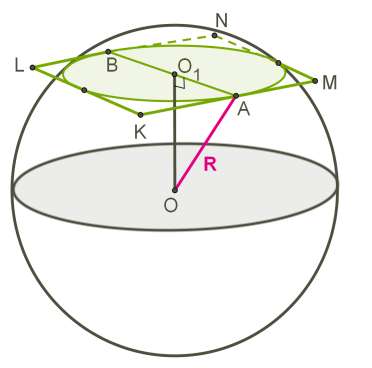
Можна отримати кулю, обертаючи круг навколо осі, що містить діаметр. Усі плоскі перерізи кулі — круги. Найбільший круг лежить в перерізі, що проходить через центр кулі, і називається великим кругом, а коло, що його обмежує - великим колом. Його радіус дорівнює радіусу кулі.
Через дві точки сферичної поверхні, розташовані на кінцях одного діаметру, можна провести безліч великих кіл.
Наприклад, через полюса Землі можна провести нескінченне число меридіанів.
Наприклад, через полюса Землі можна провести нескінченне число меридіанів.

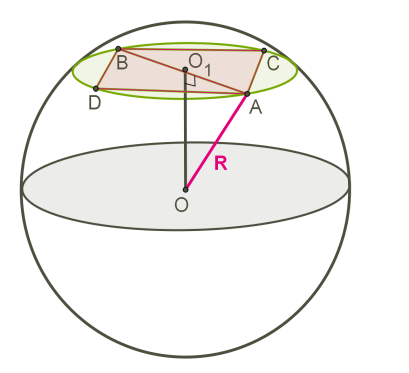
Усякий переріз кулі площиною є круг, сфери - коло (або точка, якщо площина дотикається до кулі).
При розв'язанні завдань зручніше замість кулі креслити одне з великих кіл, а площину перерізу замінити хордою цього кола.
При розв'язанні завдань зручніше замість кулі креслити одне з великих кіл, а площину перерізу замінити хордою цього кола.
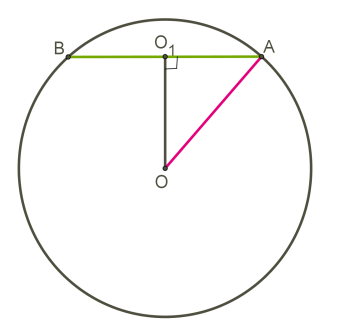
Переріз кулі площиною ділить його на два кульових сегмента, а сферу — на два сферичних сегмента.

Частина кулі, обмежена двома паралельними перерізами, називається кульовою зоною.
Кульовий сегмент обмежений кругом, який називається основою, і сферичним сегментом.
Відрізок діаметра, перпендикулярний до основи кульового (сферичного) сегмента, що міститься між основою і сферою, називають висотою кульового (сферичного) сегмента
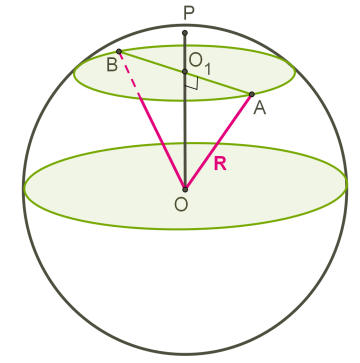
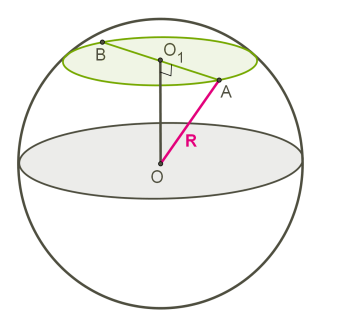
\(= d\) — відстань між центром кулі і площиною перерізу,
\(OA = R\) — радіус кулі,
\(= r\) — радіус кола перерізу.
В обчисленнях використовується теорема Піфагора в прямокутному трикутнику .