Якщо у піраміди одне ребро перпендикулярно площині основи, то вершина піраміди проектується в одну з вершин основи.
На малюнку дано трикутну піраміду з ребром \(DA\), перпендикулярним основі.
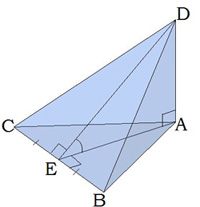
\(DA\) — перпендикулярне основі ребро, \(DA\) також є висотою,
\(DAC\) і \(DAB\) — прямокутні, кут \(DEA\) — двогранний кут при основі.
На наступному малюнку дано піраміду, основа якої — прямокутник.
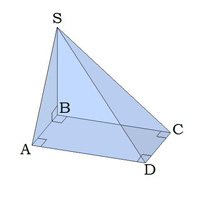
Ребро \(SB\) перпендикулярно основі, \(SB\) також є висотою,
\(SBA\) і \(SBC\) — прямокутні,
якщо основа — прямокутник, тоді \(SAD\) і \(SCD\) — прямокутні.
якщо основа — прямокутник, тоді \(SAD\) і \(SCD\) — прямокутні.
Приклад:
У завданні це потрібно доводити за допомогою теореми про три перпендикуляри ТТП — пряма, яка проведена на площині через основу похилої перпендикулярно до її проекції на цю площину, перпендикулярна і до самої похилої.
Якщо пряма \(AD\) перпендикулярна проекції похилої \(AB\), тоді вона перпендикулярна і похилій \(SA\).
Якщо пряма \(CD\) перпендикулярна проекції похилої \(BC\), тоді вона перпендикулярна і похилій \(SC\).
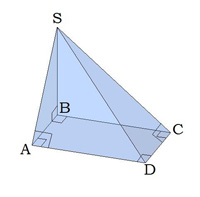
Якщо пряма \(AD\) перпендикулярна проекції похилої \(AB\), тоді вона перпендикулярна і похилій \(SA\).
Якщо пряма \(CD\) перпендикулярна проекції похилої \(BC\), тоді вона перпендикулярна і похилій \(SC\).

Записуємо за допомогою символів:
,
отже, \(SAD =\) і \(SAD\) — прямокутний.
Подібним чином доводиться, що \(SCD\) — прямокутний:
Зверни увагу!
У таких пірамід площа бічної поверхні дорівнює сумі площ всіх бічних граней
Не можна використовувати формулу правильної піраміди.
