Діагональ призми — це відрізок, який з'єднує дві вершини, які не належать одній грані.
Діагональ не існує тільки у трикутної призми.
Якщо діагоналі основи прямої призми рівні, тоді діагоналі самої призми теж рівні.
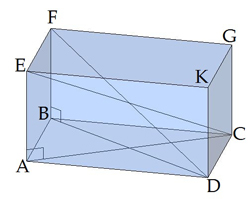
Наприклад, у куба, правильної чотирикутної призми, прямокутного паралелепіпеда діагоналі рівні \(DF = EC\), оскільки \(DB = CA\),
а у паралелепіпеда, в основі якого знаходиться паралелограм, діагоналі тільки попарно рівні , оскільки
Зверни увагу!
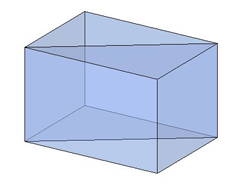
Об'ємні малюнки прямокутного і прямого паралелепіпедів не відрізняються.
Діагональний переріз призми — це переріз площиною, що проходить через два бічних ребра, які не належать одній грані.
Кожний діагональний переріз містить дві діагоналі призми.
Діагональний переріз прямої призми є прямокутником.
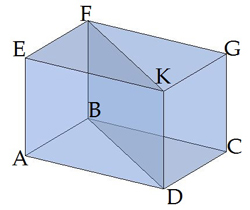
Діагональний переріз похилої призми — паралелограм.
Зверни увагу!
У правильного шестикутника діагоналі бувають двох видів — короткі і довгі.
У зв'язку з цим існує два види діагональних перерізів шестикутної призми:
У зв'язку з цим існує два види діагональних перерізів шестикутної призми:
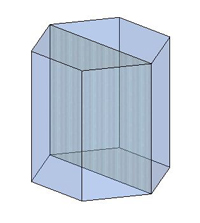
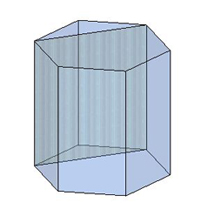
Приклад:
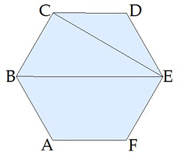
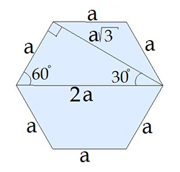
Як знайти діагоналі правильного шестикутника, якщо відома довжина його сторони?
\(CE\) — одна з коротких діагоналей шестикутника, \(BE\) — одна з довгих діагоналей.
Враховуючи те, що кути правильного шестикутника дорівнюють \(120\) градусів,
легко знайти прямокутний трикутник, в якому є кут \(30\) градусів, й використати співвідношення в цьому трикутнику.
\(CE\) — одна з коротких діагоналей шестикутника, \(BE\) — одна з довгих діагоналей.
Враховуючи те, що кути правильного шестикутника дорівнюють \(120\) градусів,
легко знайти прямокутний трикутник, в якому є кут \(30\) градусів, й використати співвідношення в цьому трикутнику.