Конус і циліндр
Циліндр є описаним навколо конуса, якщо одна його основа співпадає з основою конуса, а в центрі другої основи знаходиться вершина конуса.
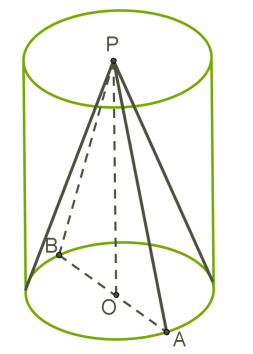
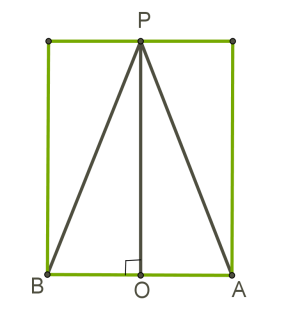
Навколо будь-якого конуса можна описати циліндр.
Осі конуса і циліндра збігаються.
Креслиться осьовий переріз.
Осі конуса і циліндра збігаються.
Креслиться осьовий переріз.
Циліндр є вписаним у конус, якщо одна його основа знаходиться в основі конуса, а друга основа стосується всіх твірних конуса.
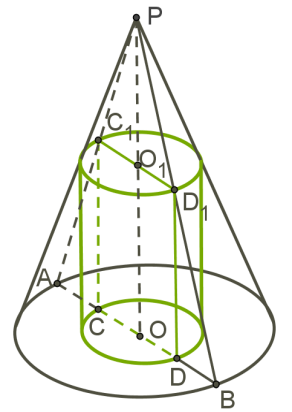
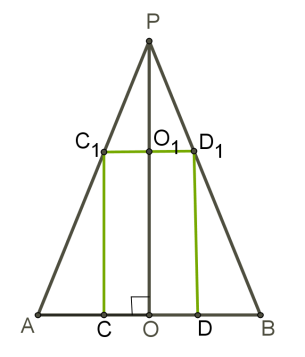
У будь-який конус можна вписати нескінченну безліч циліндрів (радіуси циліндрів менше радіуса конуса).
Креслиться осьовий переріз.
Центри основ конуса і циліндра співпадають, а висота і радіуси відрізняються.
Щоб визначити залежність між радіусами або висотами конуса і циліндра, в задачі має бути присутня додаткова інформація.
Креслиться осьовий переріз.
Центри основ конуса і циліндра співпадають, а висота і радіуси відрізняються.
Щоб визначити залежність між радіусами або висотами конуса і циліндра, в задачі має бути присутня додаткова інформація.
Конус і піраміда
Пірамідою, описаною навколо конуса, називається піраміда, основою якої є багатокутник, описаний навколо основи конуса, а вершина співпадає з вершиною конуса.
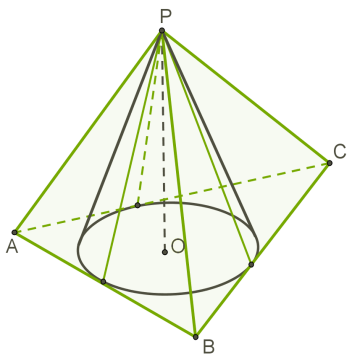
Навколо конуса можна описати тільки таку піраміду, у якої двогранні кути при основі рівні (за умови, що основа висоти піраміди не знаходиться поза багатокутником в основі піраміди).
Двогранні кути при основі рівні у правильних пірамід і у таких пірамід, висота яких проектується в центр описаного кола.
Двогранні кути при основі рівні у правильних пірамід і у таких пірамід, висота яких проектується в центр описаного кола.
Радіус конуса — радіус кола, вписаного в багатокутник основи піраміди.
Будь-яку правильну піраміду можна описати навколо конуса.
Коло основи конуса вписане в багатокутник основи піраміди.
Будь-яку правильну піраміду можна описати навколо конуса.
Коло основи конуса вписане в багатокутник основи піраміди.
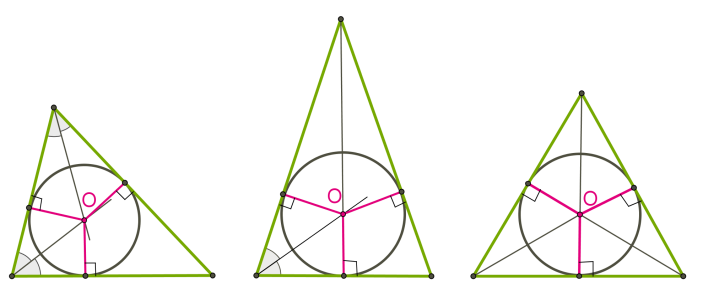
Центр вписаного в трикутник кола є точкою перетину його бісектрис. У будь-який трикутник можна вписати коло.
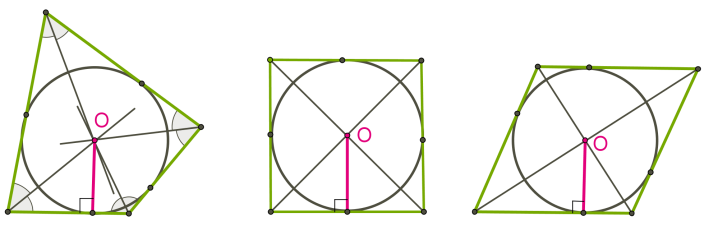
Центр вписаного в чотирикутник кола є точкою перетину його бісектрис. Коло можна вписати тільки в такий чотирикутник, у якого рівні суми довжин протилежних сторін.
Центр кола, вписаного в квадрат і в ромб, лежить на перетині його діагоналей.
Центр кола, вписаного в квадрат і в ромб, лежить на перетині його діагоналей.
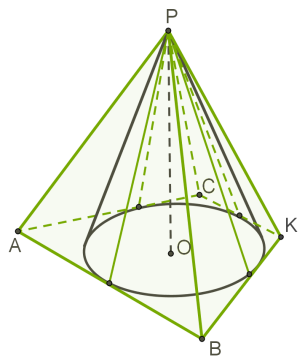
Пірамідою, вписаною в конус, називається така піраміда, багатокутник основи якої вписаний в коло основи конуса, а вершиною є вершина конуса.
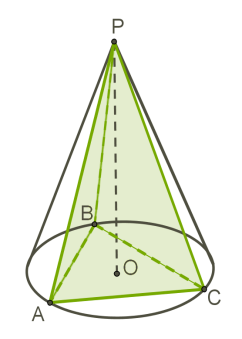
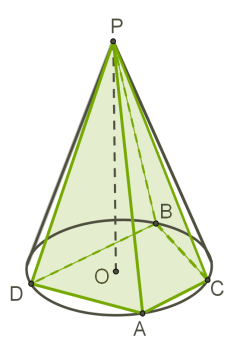
У конус можна вписати тільки таку піраміду, бічні ребра якої рівні (співпадають з твірними конуса).
Бічні ребра рівні у будь-якої правильної піраміди і у таких пірамід, висота яких проектується в центр описаного кола.
Бічні ребра рівні у будь-якої правильної піраміди і у таких пірамід, висота яких проектується в центр описаного кола.
Малюнки створюються в залежності від змісту завдання, іноді досить зобразити тільки основи цих тіл, оскільки висоти піраміди і конуса рівні.
Коло основи конуса описане навколо багатокутника основи піраміди.
Радіус конуса — радіус кола, описаного навколо багатокутника основи піраміди.
Радіус конуса — радіус кола, описаного навколо багатокутника основи піраміди.
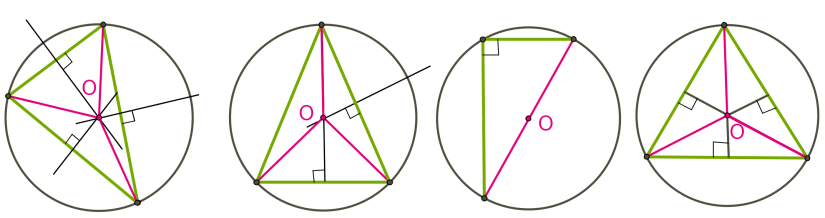
Центром кола, описаного навколо трикутника, є точка перетину серединних перпендикулярів до сторін трикутника.
Коло можна описати навколо будь-якого трикутника.
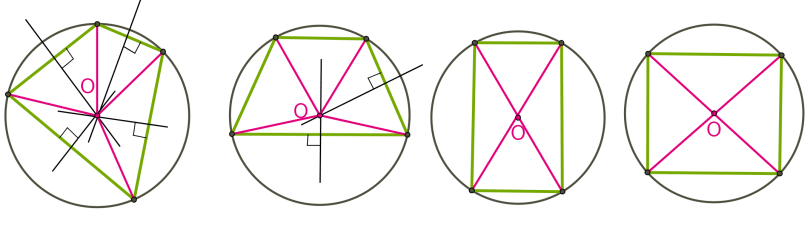
Центром кола, описаного навколо чотирикутника є точка перетину серединних перпендикулярів до сторін чотирикутника.
Коло можна описати лише навколо такого чотирикутника, у якого суми протилежних кутів дорівнюють .
Коло можна описати лише навколо такого чотирикутника, у якого суми протилежних кутів дорівнюють .
Коло можна описати навколо всіх рівнобедрених трапецій, прямокутників і квадратів.