Точка, що лежить на прямій, ділить пряму на дві частини, кожна з яких називається променем, що виходить із цієї точки. Цю точку називають початком кожного з променів.
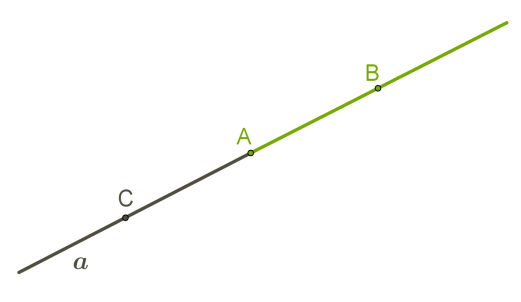
Точка \(A\) ділить пряму \(a\) на два промені. Оскільки важливо розуміти, який із променів розглядаємо, поставимо на прямій іще дві точки: \(B\) і \(C\). Назвемо промені: промінь \(AB\) і промінь \(AC\).
Зверни увагу!
Першою завжди називають початкову точку променя.
На цьому рисунку кожна з точок може бути початковою точкою певного зображеного променя. З кожної точки виходять два промені в протилежні напрямки і, подібно до прямої, продовжуються нескінченно.
Зверни увагу!
Промінь \(BC\) — той самий промінь \(AC,\) але промінь \(BC\) відрізняється від променя \(AC.\) Ці промені мають певну спільну частину.
Два різні промені однієї прямої зі спільною початковою точкою називаються доповняльними променями.
\(ВА\) та \(ВС\) — доповняльні промені з початком у точці \(В\).
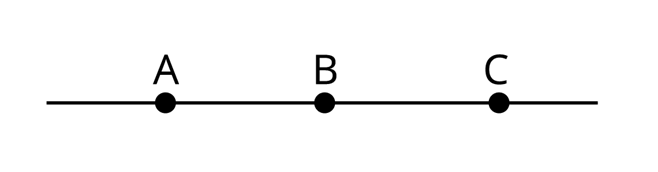
Зверни увагу!
Об'єднавши промені \(СА\) та \(АС,\) ми також отримаємо пряму \(АС.\) Проте ці промені не є доповняльними: у них немає спільного початку.
