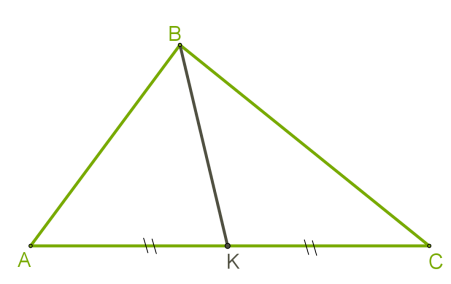
Медіана трикутника — це відрізок, що сполучає вершину трикутника із серединою протилежної сторони.
Для побудови медіани необхідно виконати такі дії:
\(1)\) Знайти середину сторони.
\(2)\) З'єднати точку, яка є серединою сторони трикутника, з протилежною вершиною трикутника. Це і буде медіана.
Зверни увагу!
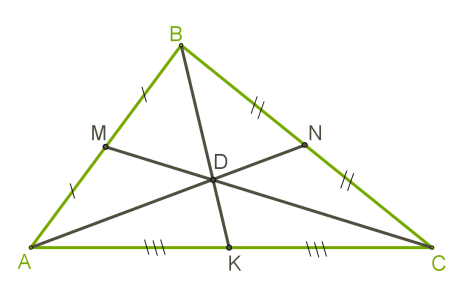
У трикутнику можна побудувати три медіани, які перетинаються в одній точці і мають такі властивості:
- Медіани трикутника перетинаються в точці, яка є його центром мас.
- Медіани трикутника зображені чорним кольором.
- Медіана поділяє трикутник на два трикутники з рівними площами (рівновеликі), а три проведені медіани — на шість рівновеликих.
- В точці перетину медіани трикутника діляться у відношенні 2:1, починаючи з вершини трикутника.
- Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи.
- В рівнобедреному трикутнику медіана кута, протилежного до основи трикутника, є його бісектрисою та висотою.
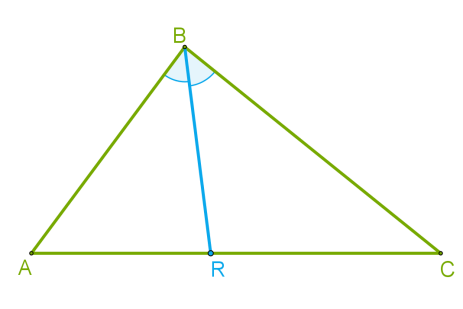
Бісектриса трикутника — це відрізок бісектриси кута трикутника, що сполучає вершину з точкою на протилежній стороні.
Для побудови бісектриси необхідно виконати такі дії:
\(1)\) Побудувати бісектрису кута трикутника (бісектриса кута — це промінь, що виходить із вершини кута й ділить його на дві рівні частини).
\(2)\) Знайти точку перетину бісектриси кута трикутника з протилежною стороною.
\(3)\) З'єднати вершину трикутника з точкою перетину бісектриси кута трикутника з протилежною стороною — цей відрізок і буде бісектрисою трикутника.
Зверни увагу!
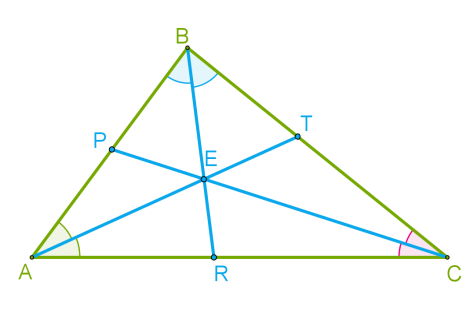
У трикутника є три бісектриси, які перетинаються в одній точці і мають такі властивості:
- Бісектриси внутрішніх кутів трикутника перетинаються в одній точці — інцентрі — центрі вписаного в цей трикутник кола.
- Бісектриси трикутника зображені голубим кольором.
- Бісектриса внутрішнього кута трикутника ділить протилежну сторону у відношенні, рівному відношенню двох прилеглих сторін.
- Якщо в трикутнику дві бісектриси рівні, то трикутник — рівнобедрений.
- В рівнобедреному трикутнику бісектриса кута, протилежного до основи трикутника, є медіаною та висотою.
- Відстані від сторін кута до будь-якої точки бісектриси однакові.
Висота трикутника — це перпендикуляр, опущений із вершини трикутника до прямої, що містить його протилежну сторону.
Для побудови висоти необхідно виконати такі дії:
\(1)\) провести пряму, яка містить одну зі сторін трикутника (у разі, якщо проводиться висота з вершини гострого кута в тупокутному трикутнику);
\(2)\) із вершини, що лежить навпроти проведеної прямої, опустити до неї перпендикуляр (перпендикуляр — це відрізок, проведений із точки до прямої, який утворює з нею кут величиною ). Це і буде висота.
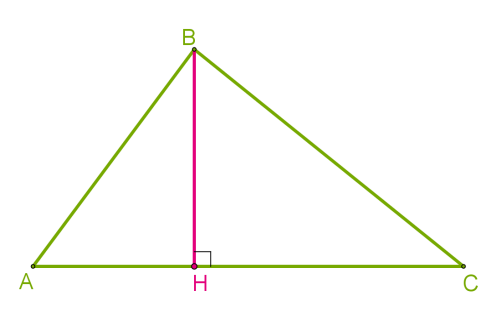
Так само, як медіани і бісектриси, трикутник має три висоти, які перетинаються в одній точці.
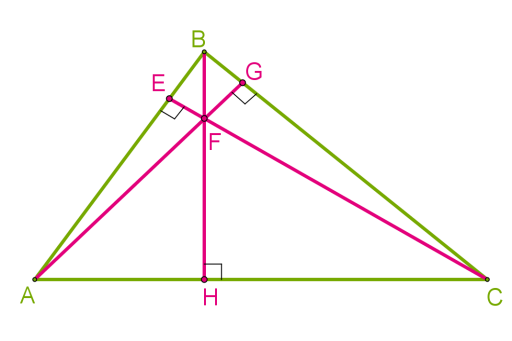
Точку перетину висот трикутника називають ортоцентром. В гострокутному він знаходиться всередині трикутника.
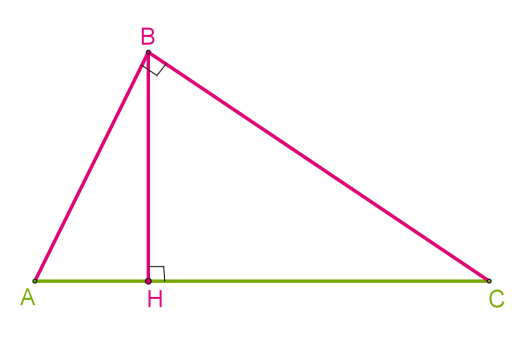
Якщо трикутник має прямий кут, то сторони, що утворюють прямий кут, можна назвати висотами, оскільки вони перпендикулярні одна до іншої. Точкою перетину висот є спільна вершина перпендикулярних сторін. Отже, в прямокутному трикутнику ортоцентр збігається з вершиною прямого кута.
Якщо трикутник має прямий кут, то сторони, що утворюють прямий кут, можна назвати висотами, оскільки вони перпендикулярні одна до іншої. Точкою перетину висот є спільна вершина перпендикулярних сторін. Отже, в прямокутному трикутнику ортоцентр збігається з вершиною прямого кута.
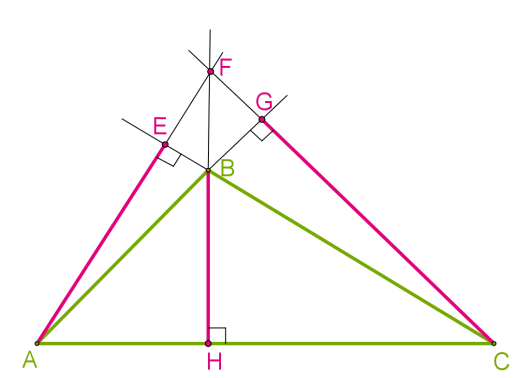
Якщо трикутник має тупий кут, то висоти, опущені з вершин гострих кутів, знаходитимуться за межами трикутника. Прямі, на яких розташовані висоти, перетинатимуться за трикутником. Отже, в тупокутному трикутнику ортоцентр лежить поза межами трикутника.
Зверни увагу!
Якщо з однієї й тієї самої вершини провести медіану, бісектрису й висоту, то медіана виявиться найдовшим відрізком, а висота — найкоротшим.
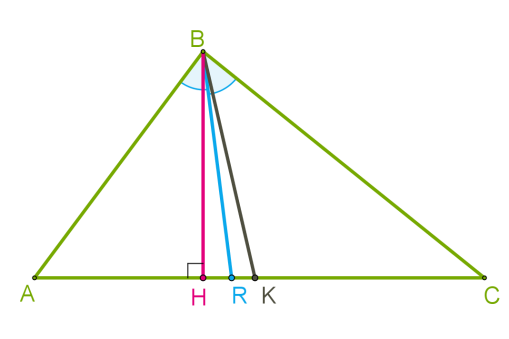
Зверни увагу!
Кожний трикутник має три висоти, три медіани й три бісектриси.
Довжини сторін трикутника, протилежних кутам \(А,\) \(В,\) \(С,\) позначають відповідно \(а,\) \(b,\) \(с.\) Довжини висот позначають \(,\) \(,\) \(,\) медіан — \(,\) \(,\) \(,\) бісектрис — \(,\) \(,\) \(.\) Індекс показує, до якої сторони проведено відрізок.
Це означає:
- Проти кута \(А\) лежить сторона \(а.\)
- До сторони \(а\) проведено висоту \(,\) медіану і бісектрису \(.\)
