Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Теорема про існування і єдиність перпендикулярної прямої
Через будь-яку точку площини можна провести пряму, перпендикулярну до даної, і тільки одну.
Через будь-яку точку площини можна провести пряму, перпендикулярну до даної, і тільки одну.
Зверни увагу!
Теорема містить два твердження:
\(1)\) існує пряма, що проходить через дану точку площини і є перпендикулярною до даної прямої;
\(2)\) така пряма єдина.
\(1)\) існує пряма, що проходить через дану точку площини і є перпендикулярною до даної прямої;
\(2)\) така пряма єдина.
Перпендикуляром до даної прямої \(a,\) проведеним із точки \(A,\) називається відрізок прямої, перпендикулярної до даної, одним із кінців якого є точка \(A,\) а другим (основою перпендикуляра) — точка перетину цих прямих \(C.\)
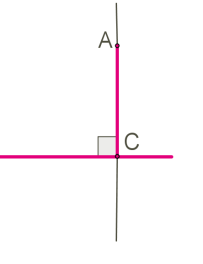
Теорема про існування і єдиність перпендикуляра до прямої.
Від точки, що не лежить на прямій, можна провести перпендикуляр до цієї прямої, причому лише один.
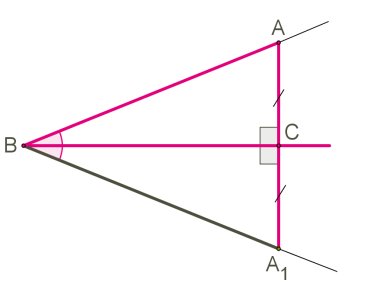
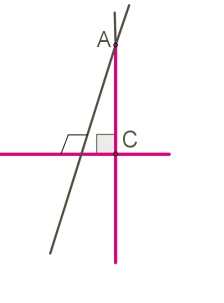
Доведемо, що від точки \(A,\) яка не лежить на прямій \(BC,\) можна провести перпендикуляр до цієї прямої.
Припустимо, що в нас є \(.\)
Відкладемо від променя \(BC\) кут, що дорівнює даному, і сумістимо ці кути за допомогою накладання. Уявімо, що складаємо аркуш паперу з рівними кутами по стороні \(BC.\)
Сторона \(BA\) суміститься зі стороною \(.\)
При цьому точка \(A\) накладеться на точку \(.\)
Отже, поєднується із \(.\)
Але і — суміжні, отже, кожен із них прямий.
Пряма перпендикулярна до прямої \(BC,\) а відрізок \(AC\) є перпендикуляром від точки \(A\) до прямої \(BC.\)
Якщо припустити, що через точку \(A\) можна провести ще один перпендикуляр до прямої \(BC,\) то він знаходитиметься на прямій, що перетинається з \(.\)
Але мають бути дві перпендикулярні прямі, відкладені до однієї й тієї самої прямої паралельними, що не можуть перетинатися.
Ми отримали суперечність. Отже, через дану точку до прямої можна провести лише один перпендикуляр.
Відстанню від точки до прямої, яка не проходить через дану точку, називається довжина перпендикуляра, проведеного з даної точки до даної прямої.