Дві фігури, які мають однакову форму та однакові розміри, називаються рівними.

Порівняння дозволяє зробити висновок про рівність фігур.
Одним зі способів порівняння фігур є накладання.
Якщо дві геометричні фігури суміщаються накладанням, вони рівні.
Як відбувається накладання відрізків \(AB\) і \(CD\)\(?\)
Кінець \(A\) одного відрізка суміщається з кінцем \(C\) другого відрізка. Якщо суміщаються й інші кінці \(B\) і \(D,\) то ці відрізки рівні: \(AB\) \(=\) \(CD.\)
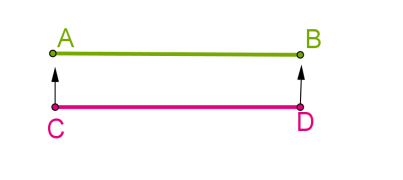
Якщо кінці відрізків не суміщаються, то один відрізок менший, ніж інший, і цей факт записують так само, як при порівнянні чисел: \(.\)

Якщо сумістити один кінець відрізка з другим, то одну половину відрізка буде поєднано з другою.
Точка, яка поділяє відрізок на дві рівні частини, називається серединою відрізка.

Якщо точка \(K\) — середина відрізка \(JL,\) то \(JK\) \(=\) \(KL.\)
Зверни увагу!
Якщо два відрізки рівні, то їхні половини рівні, і навпаки, якщо половини двох відрізків рівні, то й самі відрізки рівні.