1. Точки, прямі та відрізки

Назва нового предмету — «геометрія» — бере початок від давньогрецьких слів «земля» та «вимірюю» і в перекладі з грецької означає «землемірство».

 

Геометрія є однією з найдавніших наук. Вона виникла у зв'язку з практичною необхідністю у вимірах, завдяки відновленню меж земельних ділянок, будівництву доріг та споруд.

 

Нині ми знаємо геометрію як науку, що вивчає властивості геометричних фігур.

 

Основними геометричними фігурами є точка і пряма, які можна уявити: точку — як найпростішу нескінченно малу фігуру, уявлення про яку можна отримати, якщо на аркуш паперу натиснути добре загостреним олівцем або на шкільну дошку — добре загостреним шматком крейди, а пряму  — як нескінченну тонку натягнуту нитку, яка тягнеться безмежно в обидві сторони. За допомогою цих основних геометричних фігур можна визначити всі інші фігури.

 

 

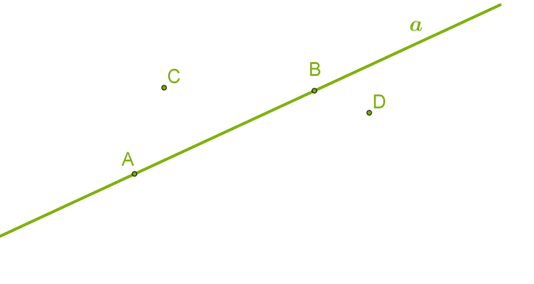
Точки позначаються великими латинськими буквами, а прямі — маленькими.  

 

Словесно описати взаємне розташування точок і прямої можна по-різному: 

 

\(1.\) Точка розташована (лежить) на прямій, або пряма проходить (проведена) через точку.

\(2.\) Точка не розташована (не лежить) на прямій, або пряма не проходить (не проведена) через точку.

 

 

\(1.\) Точки \(A\) і \(B\) розташовані (лежать) на прямій \(a\), або пряма \(a\) проходить (проведена) через точки \(A\) і \(B\)\(:\)

 

 

\(2.\) Точки \(C\) і \(D\) не розташовані (не лежать) на прямій \(a\), або пряма \(a\) не проходить (не проведена) через точки \(C\) і \(D\)\(:\)  

 

Отже, іноді позначити пряму можна і двома великими латинськими буквами, наприклад пряма \(AB,\) оскільки жодна інша пряма через ці дві точки не може бути проведена.

 

 

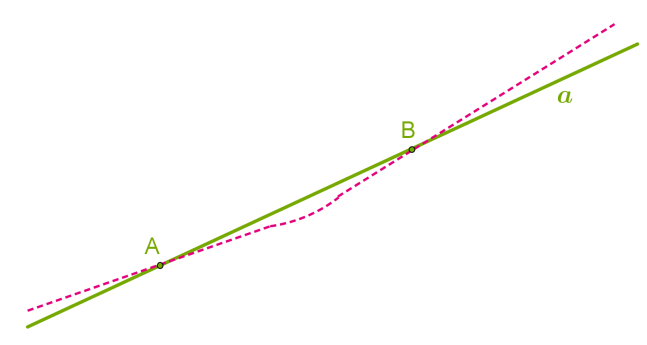
Отже, дві різні прямі можуть мати лише одну спільну точку й перетинатися або не мати жодної спільної точки і ніколи не перетинатися.

 

 

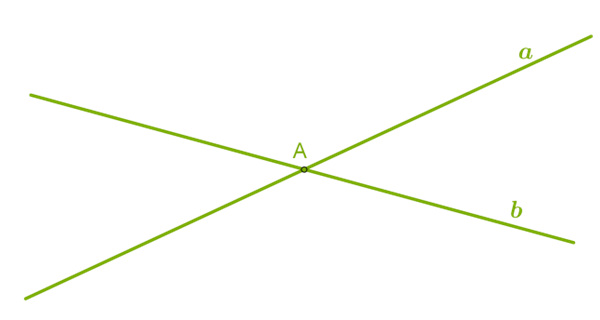
Символічно записуємо: $a\cap b=A$

 

 

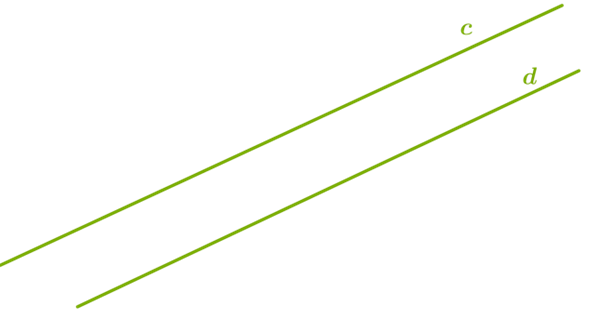
Символічно записуємо: $a\parallel b$

Уважно подивися на рисунок!