Перша ознака рівності трикутників
Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні.
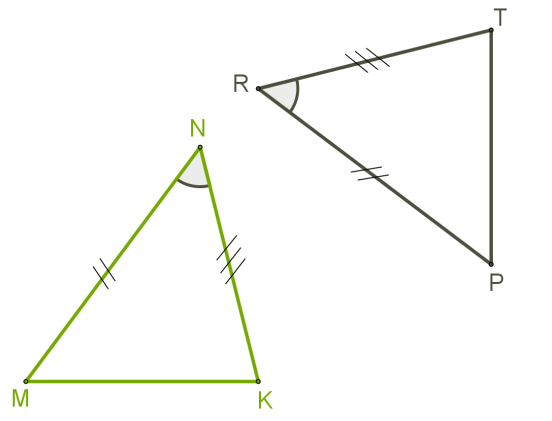
Чи достатньо цієї інформації для доведення рівності трикутників? Чи можна накласти фігури одна на одну?
\(1.\) Оскільки \(,\) то можна накласти на так, що вершина \(N\) суміститься з вершиною \(R,\) а сторони \(NM\) і \(NK\) сумістяться, відповідно, з променями \(RP\) і \(RT.\)
\(2.\) Оскільки \(,\) то сторона \(MN\) суміститься зі стороною \(PR\), а сторона \(KN\) — зі стороною \(TR.\) Зокрема, сумістяться точки \(M\) і \(P,\) \(K\) і \(T.\)
\(3.\) Сумістяться сторони \(MK\) і \(PT.\) Отже, і повністю накладаються, тому вони рівні.