
Визначення та доведення ознак паралельності прямих на площині
Дві різні прямі, що лежать на одній площині, мають лише одну спільну точку, або не мають жодної спільної точки.
У першому випадку говорять, що прямі перетинаються, у другому — що прямі не перетинаються.
Дві прямі \(a\) і \(b\) на площині, які не перетинаються, називаються паралельними і позначаються \(.\)
Зверни увагу!
Якщо розглядати прямі, які не лежать на одній площині, то можлива ситуація, що прямі не перетинаються, але й не є паралельними. Такі прямі називаються мимобіжними.

Два відрізки називаються паралельними, якщо вони лежать на паралельних прямих.
Аксіома паралельних прямих (аксіома Евкліда)
Через точку, що не лежить на даній прямій, можна провести пряму, паралельну даній, і до того ж тільки одну.
Через точку, що не лежить на даній прямій, можна провести пряму, паралельну даній, і до того ж тільки одну.
Ознаки паралельності прямих на площині.
\(1.\) Дві прямі, паралельні третій, паралельні між собою.
\(2.\) Якщо дві прямі на площині перпендикулярні до однієї й тієї самої прямої, вони паралельні.
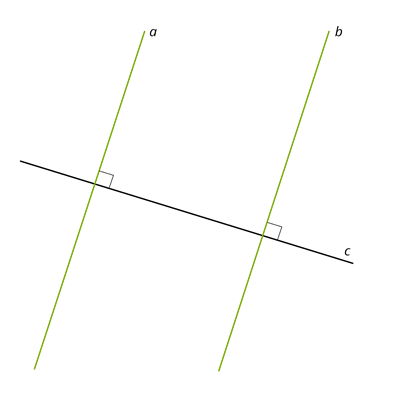
Цю ознаку легко довести, якщо згадати, що до прямої на площині з будь-якої точки можна провести лише один перпендикуляр.
Припустимо, що прямі, перпендикулярні до однієї й тієї самої прямої, не є паралельними, тобто мають спільну точку.
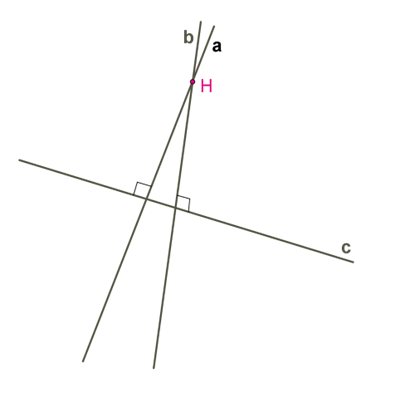
Виникає суперечність: із однієї точки \(H\) до прямої \(c\) проведено два перпендикуляри. Таке неможливо, тому дві прямі на площині, перпендикулярні до однієї й тієї самої прямої, є паралельними.
Щоб розглянути інші ознаки, потрібно ознайомитися з деякими видами кутів
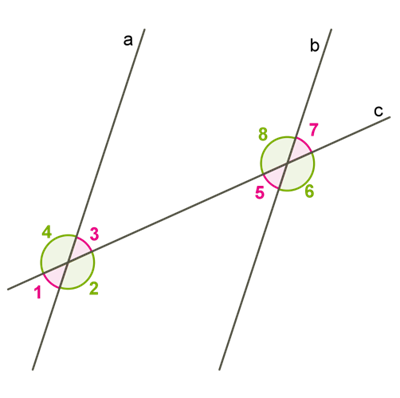
\(1.\) Пригадаємо, які нам відомі назви та властивості кутів, утворених двома прямими, що перетинаються.
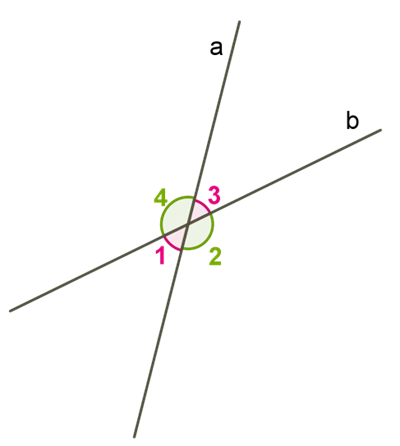
Вертикальні кути рівні:
Сума суміжних кутів складає \(:\)
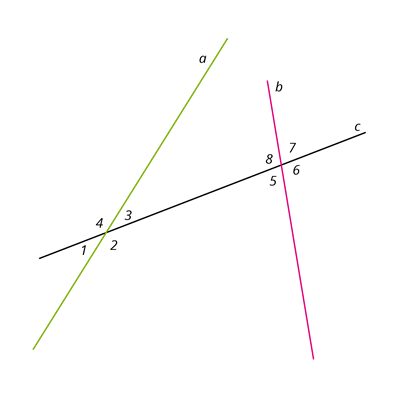
Нехай пряма \(c\) перетинає прямі \(a\) і \(b\) у двох різних точках. У такому разі кажуть, що пряма \(c\) є січною прямих \(a\) і \(b\). У результаті такого перетину двох прямих третьою утворюються пари нерозгорнутих кутів, які мають спеціальні назви:
- внутрішні різносторонні кути лежать між прямими \(a\) і \(b\) по різні боки від січної:
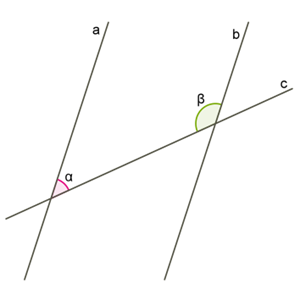
- внутрішні односторонні кути лежать між прямими \(a\) і \(b\) по один бік від січної:
- відповідні кути лежать по один бік від січної, причому сторона одного з них є частиною сторони другого:
Ці кути допоможуть визначити паралельність прямих \(a\) і \(b.\)
Доведемо ще кілька ознак паралельності прямих:
Якщо при перетині двох прямих січною виконується принаймні одна з умов:
\(1)\) внутрішні різносторонні кути рівні;
\(2)\) сума внутрішніх односторонніх кутів дорівнює \(180 °;\)
\(3)\) відповідні кути рівні,
то дані прямі паралельні.
\(1)\) внутрішні різносторонні кути рівні;
\(2)\) сума внутрішніх односторонніх кутів дорівнює \(180 °;\)
\(3)\) відповідні кути рівні,
то дані прямі паралельні.
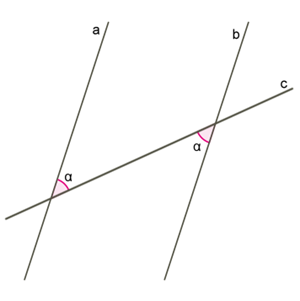
Доведемо цю ознаку.
Якщо при перетині прямих \(a\) і \(b\) прямою \(c\) внутрішні різносторонні кути рівні, то прямі \(a\) і \(b\) паралельні.
Наприклад, якщо \(,\) то \(.\)
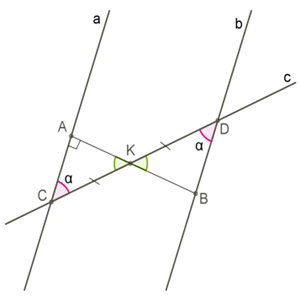
\(1.\) Позначимо точки \(C\) і \(D,\) у яких прямі \(a\) і \(b\) перетинає пряма \(c.\) Через середину відрізка \(CD\) точку \(K\) цього відрізка проведемо перпендикуляр \(AB\) до прямої \(a.\)
\(2.\) \(=\) як вертикальні кути, \(=\) \(=\) \(,\) \(CK = KD,\) отже \(=\) за ознакою про сторону та два кути.
\(3.\) Зрозуміло, що якщо прямокутний, то й прямокутний, і \(AB\) перпендикулярний до прямої \(b.\)
\(4.\) Прямі, перпендикулярні до однієї й тієї самої прямої, є паралельними (відповідно до першої доведеної ознаки).
\(5.\) У випадку, коли відповідні кути рівні, маємо на увазі, що вертикальні кути рівні, і доводимо, як у пунктах \(1–4.\)
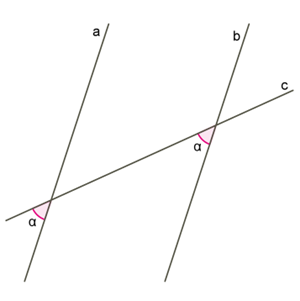
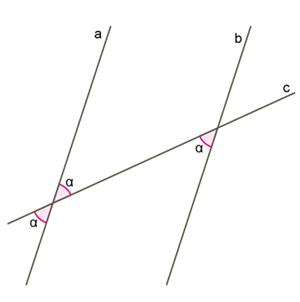
\(6.\) У випадку, коли сума внутрішніх односторонніх кутів дорівнює \(180°,\) маємо на увазі, що сума суміжних кутів також дорівнює \(180°\) і використовуємо в доведенні пункти \(1–4.\)
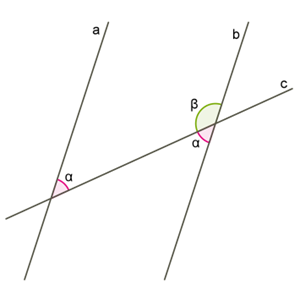
Ознака паралельних прямих діє і як властивість паралельних прямих.
При перетині двох паралельних прямих третьою січною:
- внутрішні різносторонні кути рівні;
- відповідні кути рівні;
- сума внутрішніх односторонніх кутів дорівнює \(180°\).