Чотирикутник, у якого протилежні сторони попарно паралельні, називається паралелограмом.
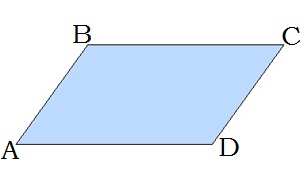
Властивості паралелограма
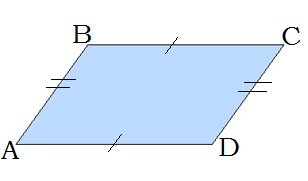
\(1.\) Протилежні сторони паралелограма рівні:
\(AB = DC,\) \(BC = AD\)
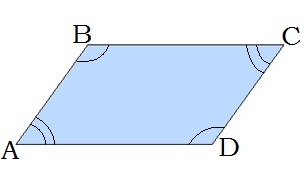
\(2.\) Протилежні кути паралелограма рівні:
\(A =\) \(C,\) \(B =\) \(D\)
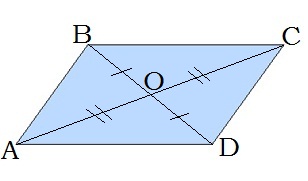
\(3.\) Діагоналі паралелограма діляться навпіл точкою перетину:
\(BO = OD,\) \(AO = OC\)
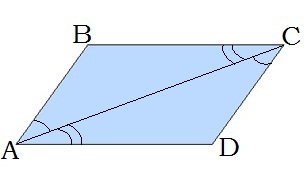
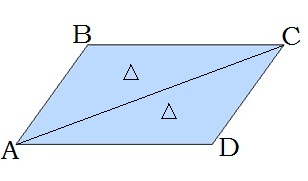
\(4.\) Діагональ ділить паралелограм на два рівні трикутники: \(ABC\) і \(CDA.\)
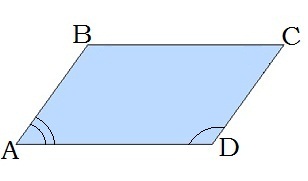
\(5.\) Сума кутів, прилеглих до кожної сторони паралелограма, дорівнює \(180°.\)
\(A\) \(+\) \(D\) \(=\) \(180\)
\(6.\) Різносторонні кути при діагоналі рівні:
\(BAC =\) \(ACD,\) \(BCA =\) \(CAD\)