Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на іншій його стороні.
Необхідно поділити відрізок \(AB\) на \(7\) рівних частин.
Намалюємо кут, на одній стороні якого лежить відрізок \(AB.\) Сторону кута \(BC\) намалюємо по клітинках і використаємо клітинки для поділу сторони на \(7\) рівних частин:
Намалюємо кут, на одній стороні якого лежить відрізок \(AB.\) Сторону кута \(BC\) намалюємо по клітинках і використаємо клітинки для поділу сторони на \(7\) рівних частин:
\(BD = DE = EF = FG = GH = HJ = JC\)
Кінці обох відрізків з'єднаємо, отримаємо \(AC.\)
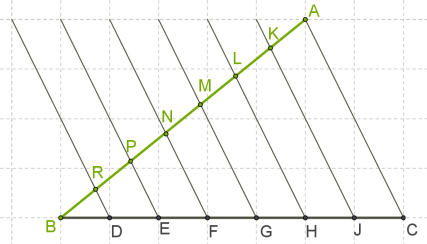
Проведемо прямі, паралельні \(AC,\) що починаються в точках \(J, H, G, F, E, D,\) отримаємо \(7\) паралельних прямих (знову використовуємо клітинки).
Якщо \(BD = DE = EF = FG = GH = HJ = JC\) і \(AC\) \(JK\) \(HL\) \(GM\) \(FN\) \(EP\) \(DR,\) то за теоремою Фалеса, \(BR = RP = PN = NM = ML = LK = KA.\)
