Два трикутники називаються подібними, якщо їхні відповідні кути рівні, а відповідні сторони пропорційні.
Маємо трикутники \(ABC\) і \(DEF.\)
Якщо відомо, що і \(,\) можна зробити висновок, що \(.\)
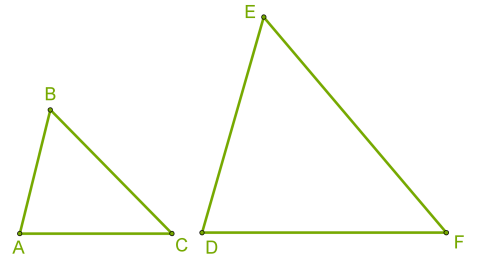
Під час запису подібності трикутників важливо дотримуватися порядку букв. Рівним кутам відповідають певні букви.
Число k, яке дорівнює співвідношенню відповідних сторін трикутників, називається коефіцієнтом подібності трикутників.
Щоб визначити, чи є трикутники подібними, необов'язково знати довжини всіх сторін і градусні міри всіх кутів трикутників. Це можна зробити простіше, використовуючи ознаки подібності трикутників.
Співвідношення периметрів двох подібних трикутників дорівнює коефіцієнту подібності трикутників:
Співвідношення площ двох подібних трикутників дорівнює квадрату коефіцієнта подібності:
