Співідношенням двох відрізків називається співвідношення їхніх довжин.
Розглянемо два відрізки \(AB\) і \(VN,\) де відрізок \(AB\) удвічі більший від другого відрізка:
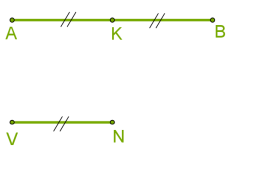
Співвідношення відрізків \(AB\) і \(VN\) дорівнює \(2 : 1\)\(/\)
Можна також сказати, що співвідношення відрізків \(VN\) і \(AB\) дорівнює \(1 : 2\)\(/\)
У цьому прикладі відрізок \(AR\) дорівнює трьом одиницям, а \(VZ\) — двом одиницям.
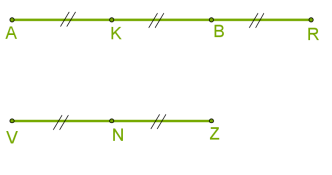
Співвідношення відрізків \(AR\) і \(VZ\) дорівнює \(3 : 2\)\(.\)
або
Якщо співвідношення відрізків \(a\) і \(b\) дорівнює співвідношенню відрізків \(c\) і \(d,\) тобто \(,\) то ці відрізки називаються пропорційними.
Розглянемо дані малюнки:


Порівняємо співвідношення відрізків \(.\)
Отже, — ці пари відрізків пропорційні.
Щоб записати співвідношення відрізків, необхідно два відрізки. Щоб знайти пропорційні відрізки, необхідно дві пари відрізків.
