1. Модуль вектора

Довжина напрямленого відрізка визначає числове значення вектора і називається довжиною або модулем вектора.
Маємо вектор AB→=x;y\(.\)
 
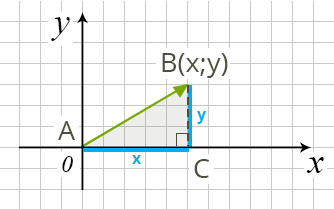
векторы-модуль-формула.png
 
Із теореми Піфагора випливає, що в трикутнику \(ABC\) довжина відрізка \(AB,\) яка є модулем вектора AB→\(,\) дорівнює AC2+CB2\(.\)
 
Отже, модуль (довжина) вектора AB→ розраховується за формулою AB→=x2+y2\(.\) 
Приклад:
Обчисли довжину вектора AB→=5;3\(.\)
 
Розв'язок: AB→=52+32=34
Відстань між двома точками
Як відомо, координати вектора можна визначити, якщо відомі координати початкової та кінцевої точок вектора Ax1;y1 і Bx2;y2\(.\)
 
AB→x2−x1;y2−y1
 
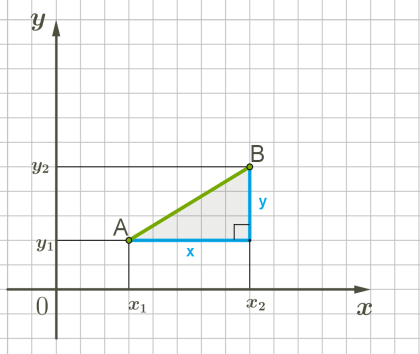
Koord_vektori_galap.png
 
Якщо x=x2−x1\(,\) y=y2−y1 і AB→=x2+y2\(,\) то на місце \(x\) і \(y\) можна поставити їхні вирази.
 
Нову формулу називають не лише формулою довжини вектора, а й формулою відстані між двома точками із заданими координатами:
 
AB=x2−x12+y2−y12
 
Оскільки вирази в дужках у квадраті, правильним є те, що:
 
AB=x2−x12+y2−y12=x1−x22+y1−y22
 
Тобто послідовність координат у різниці не важлива.
 
Зверни увагу!
Якщо дано координати початкової і кінцевої точок вектора Ax1;y1 і Bx2;y2\(,\) то AB→x2−x1;y2−y1\(.\)
 
Від координат кінцевої точки обов'язково потрібно віднімати координати початкової точки!
  
Але при визначенні довжини вектора у формулі послідовність координат не має значення:
 
AB→=x2−x12+y2−y12=x1−x22+y1−y22
Попередня тема
Повернутись до теми
Наступна теорія
Copyright © 2026 «МійКлас»