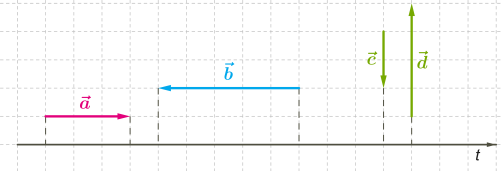
Проекція вектора
У математиці існує два визначення:
\(1)\) геометрична проекція вектора — вектор;
\(2)\) проекція вектора на вісь — число.
Геометрична проекція вектора — це вектор, який можна отримати, якщо провести перпендикуляри від кінців вектора до вибраної осі. Проекція початку вектора відповідає початку геометричної проекції, а проекція кінця вектора — кінцю геометричної проекції.
Для вектора геометрична проекція на осі \(t\) — це вектор \(.\)
Для вектора геометрична проекція на осі \(y\) — це вектор \(.\)
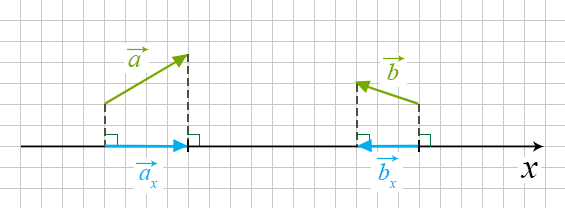
Проекція вектора на вісь — це скалярна величина (число), що дорівнює довжині геометричної проекції вектора, якщо напрями осі й геометричної проекції збігаються; або число, протилежне довжині геометричної проекції вектора, якщо напрями геометричної проекції та осі — протилежні.
Якщо довжина вектора дорівнює і — це гострий кут, утворений вектором та віссю \(x,\) то скалярна проекція вектора обчислюється за формулою \(.\)
Знак проекції вектора вибирається залежно від напряму осі.
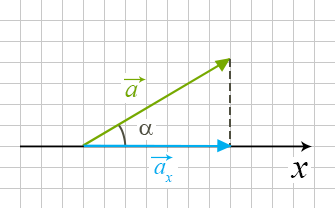
На малюнку ми бачимо, що цю формулу можна отримати зі співвідношення в прямокутному трикутнику:
Зверни увагу!
Якщо вектор і вісь проекцій паралельні, то скалярна проекція на цій осі є числом, яке дорівнює довжині вектора.
Якщо напрями вектора і осі збігаються або число є протилежним довжині вектора, то напрями вектора і осі — протилежні.
Якщо вектор і вісь проекцій перпендикулярні, то проекція вектора на цій осі дорівнює \(0.\)