Паралельне перенесення
Паралельним перенесенням фігури називається перенесення всіх точок простору на одну відстань в одному напрямі.
Паралельне перенесення визначає вектор, за яким відбувається перенесення.
Щоб здійснити паралельне перенесення, потрібно знати напрям і відстань, що означає задати вектор.
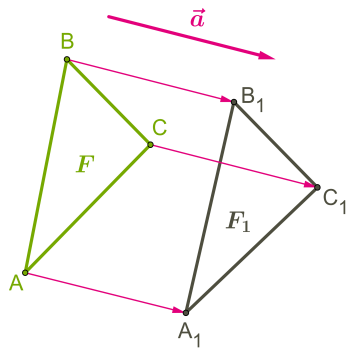
Аби при паралельному перенесенні побудувати зображення многокутника, достатньо побудувати зображення вершин цього многокутника.
Початкова фігура та фігура, отримана після паралельного перенесення, рівні.
Паралельне перенесення використовується для конструювання графіків функцій.
На малюнку зображена парабола і два результати паралельного перенесення.
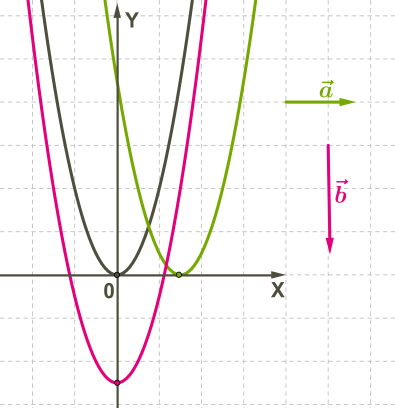
Іноді паралельне перенесення зустрічається в незвичних ситуаціях.

Поворот
Якщо одна фігура отримана з іншої фігури поворотом усіх її точок щодо центру \(O\) на один і той самий кут в одному й тому самому напрямі, то таке перетворення фігури називається поворотом.
Проти годинникової стрілки буде додатний кут повороту, а за годинниковою стрілкою — від'ємний (так само, як кути повороту в одиничному колі).
Трикутник \(ABC\) повернений у додатному напрямі (приблизно на \(=\) \(45°\)).
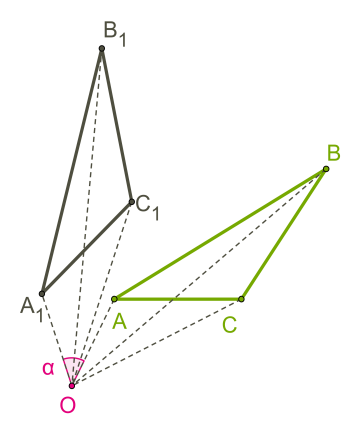
Якщо кут повороту дорівнює \(180°\) або \(-180°,\) то фігура відображається як центрально симетрична даній, і цей поворот називається центральною симетрією.
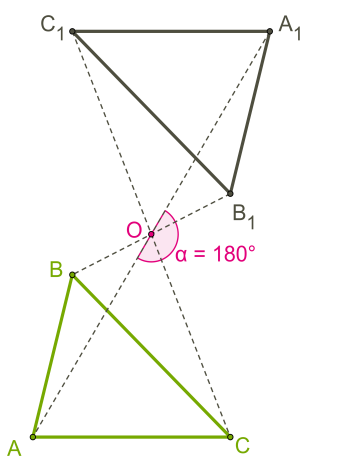
Площина покрита фігурами, які взаємно повернені.
