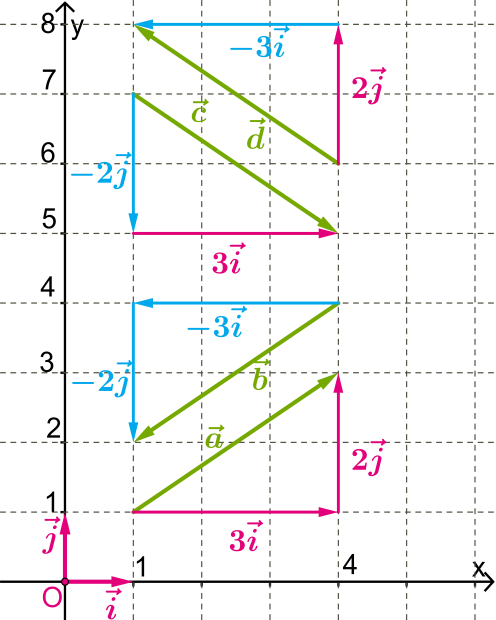
Згадаймо, що при множенні вектора на число ми отримуємо два колінеарних (паралельних) вектори, які або співнапрямлені, якщо \(,\) або протилежно напрямлені, якщо \(.\)
Довжини векторів відрізняються у \(k\) разів.
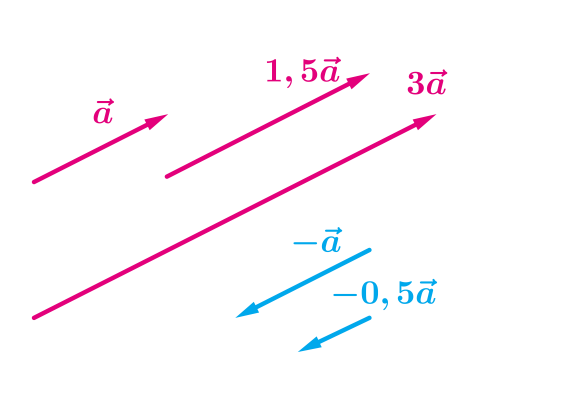
Правильним є і протилежне твердження:
Якщо ненульові вектори колінеарні, то обов'язково можна знайти число так, що \(.\)
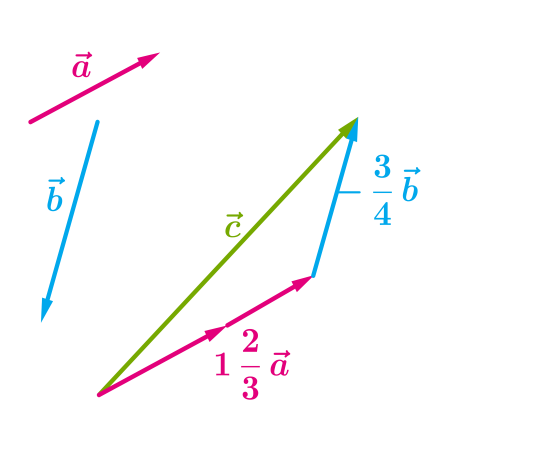
Для неколінеарних векторів правильним є твердження, що кожен вектор на площині можна зобразити у вигляді \(.\)
Кажуть, що вектор розкладений за векторами і \(,\) а числа \(k\) і \(m\) називають коефіцієнтами розкладання.
Це правильно для будь-якого вектора на площині, причому коефіцієнти визначаються єдиним чином.
Виберемо два неколінеарних вектори на осях системи координат. Нехай довжина кожного з них буде дорівнювати одиничному відрізку в цій системі координат. Ці вектори називають координатними векторами і позначають та \(.\)
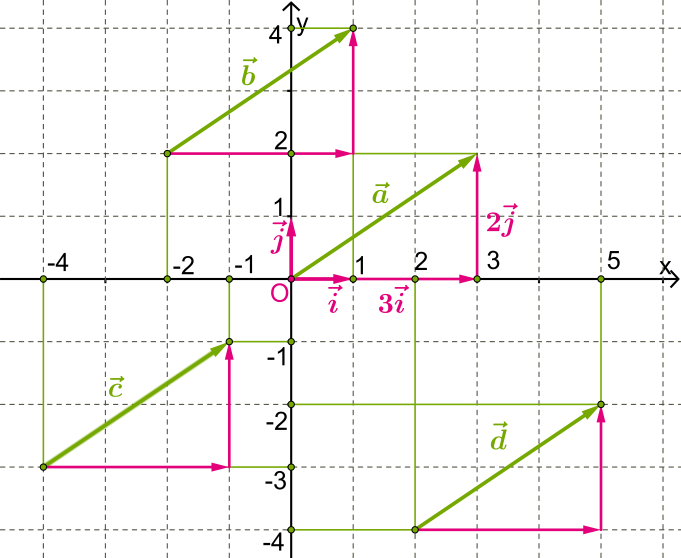
Якщо від початку координат відкласти вектор \(,\) то його можна розкласти за векторами та наступним чином:
У цьому розкладанні коефіцієнти координатних векторів називаються координатами вектора \(.\)
Будь-який вектор, що дорівнює вектору \(,\) можна перемістити і відкласти від початку координат. Отже, можемо зробити висновок:
Рівні вектори мають рівні координати.
Але в той же час у координатній системі можна перемістити вектори і \(,\) і таким чином визначити координати векторів незалежно від їх місця розташування в координатній системі.
Легко зрозуміти, що різниця між абсцисами (координатами \(x\)) кінцевої і початкової точки вектора і є абсцисою вектора, а різниця між ординатами (координатами \(y\)) кінцевої і початкової точки вектора є ординатою вектора.
Зв'язок між координатами протилежних векторів випливає з того, що якщо помножити вектор на \(-1,\) результатом буде протилежний вектор.
У протилежних векторів протилежні координати.
Важливо зрозуміти ще кілька цікавих зв'язків між координатами векторів однакової довжини.