Щоб зменшити будь-яке число на \(n\) одиниць, потрібно від цього числа відняти \(n\) одиниць.
Зменшити число \(6\) на \(2\):
У цьому випадку число, яке потрібно зменшити — це \(6\), а \(n\) —це \(2\).
Отже, .
У Петрика було \(6\) цукерок, а у Надійки на \(2\) цукерки менше. Скільки цукерок було у Надійки?
Щоб розв'язати цю задачу, потрібно зменшити кількість цукерок у Петрика на \(2\).
 \(-\)
\(-\)  \(=\)
\(=\) 
Відповідь: \(4\) цукерки.
Щоб зменшити будь-яке число в(у) \(n\) разів, потрібно поділити це число на \(n\).
Приклад:
Зменшити число \(8\) у \(4\) рази:
У цьому випадку число, яке потрібно зменшити \(8\), а \(n\) це — \(4\).
Отже, .
У цьому випадку число, яке потрібно зменшити \(8\), а \(n\) це — \(4\).
Отже, .
Було \(8\) шматочків піци, цю кількість зменшили у \(4\) рази. Скільки шматків піци стало?

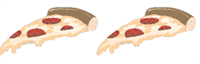
Відповідь: \(2\) зірочки.
