 |
Зараз ми, разом із тобою, пригадаємо прийоми множення і ділення трицифрових чисел на одноцифрове число. |
І, для початку, ми повинні пригадати властивості множення та ділення на \(1, 10, 100\).
Властивості множення і ділення на \(0, \)\(1, 10, 100\).
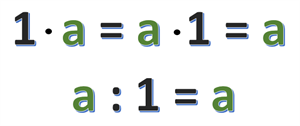
При множенні/діленні будь-якого числа на одиницю, отримаємо те саме число: \(а · 1 = а; а : 1 = а\)
Приклад:
\(354 · 1 = 354\)
\(925 : 1 = 925\)
Щоб помножити будь-яке число на \(10\), справа від цього числа потрібно дописати нуль, а при множенні на \(100\) — два нулі.
Приклад:
\(74 · 10 = 740\)
\(6 · 100 = 600\)
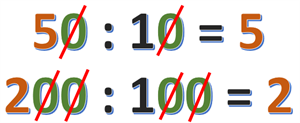
Щоб поділити будь-яке число на \(10\), справа від цього числа нам потрібно прибрати нуль, а щоб поділити на \(100\) — два нулі.
Приклад:
\(650 : 10 = 65\)
\(300 : 100 = 3\)
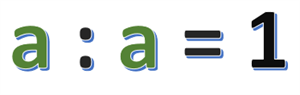
Якщо будь-яке число поділити на це саме число, то в результаті отримаємо \(1\).
Приклад:
\(78 : 78 = 1\)
\(925 : 925 = 1\)
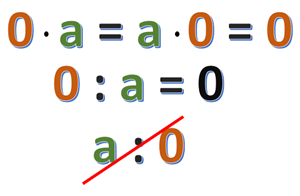
При множенні будь-якого числа на нуль, отримаємо нуль.
Ділити на нуль не можна!
Приклад:
\(0 : 478 = 0 \)
\(354 · 0 = 0 · 354 = 0\)
\(670 : 0\) — ділити не можна