2. Метод підстановки

— Графічний спосіб.
  
При виборі цього способу, потрібно побудувати графіки цих рівнянь і знайти точки їх перетину.
 
Розв'яжи систему рівнянь.
 
2y−5x=6,3y+2x=4.
 
Розглянь перше рівняння системи 2y — 5x = 6.
 
x
0
-2
y
3
-2
 
Розглянь друге рівняння системи  3y + 2x = 4.
 
x
2
-4
y
0
4
 
Побудуй графіки рівнянь по точкам і знайди точку перетину.
 
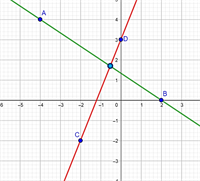
Рисунок74.png
 
Відповідь: ( -1,6; 1,8).
 
Зверни увагу!
Даний спосіб завжди дає результат, але у більшості випадків він приблизний. Тому цей метод найчастіше застосовують тоді, коли треба вказати кількість розв'язків.
Найчастіше у шкільному курсі ми зустрічаємось з системами лінійних рівнянь. Але системи рівнянь можуть бути  ірраціональними, тригонометричними … в залежності від того які рівняння входять в склад системи. Для розв'язання таких систем можна використовувати способи описані раніше, а також існують інші способи і методи.
 
Розглянемо найдієвіший.
  
— Спосіб підстановки.
 
При використанні даного методу більш складні математичні вирази замінюємо на певні змінні, в результаті ми можемо прийти до системи лінійних рівнянь або до системи більш простих рівнянь.
Приклад:
Розв'яжи систему рівнянь.
5x4+y4=17x2+y2,x2−xy+y2=7;5x2+y22−10x2y2=17x2+y2,x2−xy+y2=7;|x2+y2=txy=m|5t2−10m2=17t,t−m=7;m=t−7,5t2−10t−72=17t.5t2−10t−72=17t,5t2−10t2+140t−490−17t=0,−5t2+123t−490=0,D=1232−4⋅−5⋅−490=5329,⇒D=73t1=−123+73−10=5,⇒m1=−2;t2=−123−73−10=19.6,⇒m2=12.6.t1=5,m1=−2;⇒x2+y2=5,xy=−2;x+y2+4=5,xy=−2;x+y2=1,xy=−2;x+y=1,xy=−2,x+y=−1,xy=−2;x=1−y,y−y2+2=0,x=−1−y,−y−y2=−2;x=1−y,y2−y−2=0,x=−1−y,y2+y−2=0;x1=−1,x2=2,y1=2,y2=−1,x1=1,x2=−2,y1=−2,y2=1.t2=19,6,m2=12,6;⇒x2+y2=19,6,xy=12,6;x+y2−25,2=19,6,xy=12,6;x+y2=44,8,xy=12,6;− сторонні розв"язки.Відповідь:(−1;2),2;−1,1;−2,−2;1.
Попередня теорія
Повернутись до теми
Наступне завдання
Copyright © 2026 «МійКлас»