Тригонометричним рівнянням називають рівність, де невідома величина тільки під знаком тригонометричних функцій і справедлива тільки при певних значеннях невідомого.
Коренями тригонометричного рівняння називають значення невідомих, які задовольняють рівнянню.
Розв'язати тригонометричне рівняння означає знайти його корені або довести, що коренів не має. Тригонометричне рівняння має безліч коренів або не має розв'язків.
Розглядають чотири види найпростіших тригонометричних рівнянь, для яких описані формули загальних розв'язків.
1.
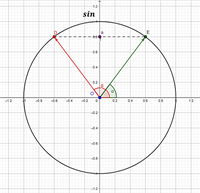
Приклад:
2.
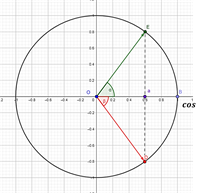
Приклад:
3.
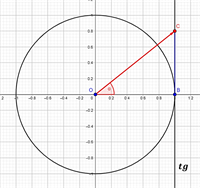
Приклад:
4.
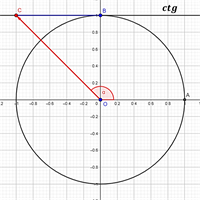
У таблиці нижче наведені окремі випадки тригонометричних рівнянь.

Розв'язання більш складних рівнянь зводяться до зведення рівняння до однієї тригонометричної функції і до одного аргументу.
Для цього використовують такі методи:
— метод підстановки;
— метод тотожних перетворень;
— зведення до квадратного;
— використання універсальної підстановки;
— використання тригонометричних тотожностей.