У процесах, що відбуваються навколо нас, багато величин змінюють свої значення. Деякі з цих величин пов'язані між собою, тобто зміна однієї величини спричиняє зміну іншої. Такі залежності називають функціональними.

У функціональній залежності одна змінна обирається довільно і називається — незалежна змінна, значення другої змінної знаходимо за відповідним правилом (формула, графік, таблиця, опис). Другу змінну називають — залежна змінна.

У математиці прийнято незалежну змінну позначати буквою \(х\), а залежну змінну — буквою \(у\). Якщо кожному значенню незалежної змінної \(х\) ставиться у відповідність тільки одне значення залежної змінної, то таку залежність називають функцією (від латинського слова functio — виконання)

Приклад:
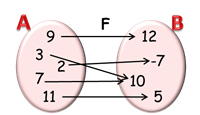
рис.\(1\)\( \)
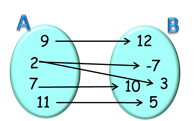
рис.\(2\)
На рис.\(1\ \)наведено приклад функції. Кожному елементу множини \(А\) поставлено у відповідність елемент мнодини \(В\). Задана залежність на рис.\(2\) не функціональна і не є функцією. Одному елементу множини \(А\) відповідає два елементи множини \(В\).

Приклад:
\(1.\) Катер пли по озеру \(t\) годин зі швидкістю \(45\) км/год і пройшов \(S\) км.
\(t\) год — аргумент функції
\(S\) км — значення функції
\(2\).
\(x\) — аргумент функції
\(y\) — значення функції
\(3\). Зміна температури води від часу нагрівання задана в таблиці
| \(t\) час | \(5\) | \(10\) | \(15\) | \(20\) |
| \(T\ \)°C | \(10\) | \(20\) | \(30\) | \(40\) |
\(t\ \) — аргумент функції
\(T\) — значення функції
Функцію вважають заданою, якщо вказано її область визначення та правило, за допомогою якого можна за кожним значенням незалежної змінної знайти значення залежної змінної.
