Функцію вважають заданою, якщо вказано її область визначення та правило, за допомогою якого можна за кожним значенням незалежної змінної знайти значення залежної змінної. В математиці розклядаю чотири способи задання функції

Приклад:
\(1.\) Описовий спосіб
Автомат щохвилини виготовляє \(12\) цукерок. Яку кількість цукерок \((N)\) виготовить автомат за \(t\ \)годин, якщо автомат працює \(18\) годин на добу?
\(2. \)Табличний спосіб
| \(t\) год | \(1\) | \(2\) | \(3\) | \(4\) |
| \(S\) км | \(60\) | \(120\) | \(180\) | \(240\) |
\(3\). Графічний спосіб
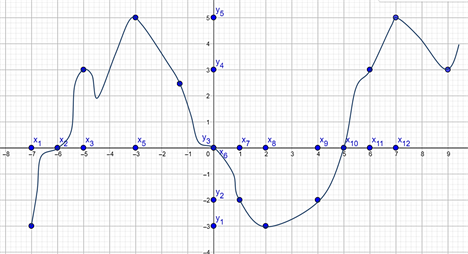
\(4\). Аналітичний спосіб:
Об'єм куба можна задати формулою , де \(а\) — довжина сторони куба ( довільне додатнє число)


Приклад:
\(1.\)
Незалежна зміння \(x\) і залежна змінна \(y\) можуть приймати довільні значення. Область визначеня функції будь—яке число і область значення функції будь—яке число.
\(2.\)
Функція представлена дробом . Даний дріб має зміст якщо . Область визначення . Область значень такої функції ти навчишся знаходити пізніше.
\(3. \) Функція задана таблично
| \(x\) | \(2\) | \(3\) | \(5\) | \(9\) |
| \(y\) | \(12\) | \(-5\) | \(9\) | \(32\) |
Область визначення: \(2; 3; 5; 9\)
Область значення: \(12; -5; 9; 32\)