Розглядаючи лінійну функцію виду \(y = kx + b\), особливо виділяють випадок, коли \(b = 0\).
Тоді лінійна функція набуває вигляду \(y = kx\).
Тоді лінійна функція набуває вигляду \(y = kx\).
Графіком лінійної функції \(y = kx\) є пряма, що проходить через початок координат.
Важливо вміти переходити від аналітичної моделі \(y = kx\) до геометричної і, навпаки, від геометричної до аналітичної моделі.
Наприклад, розглянемо пряму, зображену на рисунку.
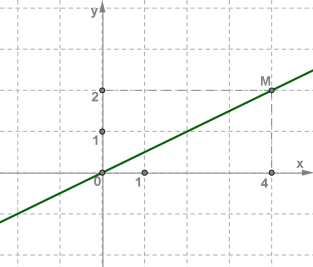
Ця пряма є графіком лінійної функції \(y = kx\), оскільки проходить через початок координат. Потрібно лише визначити значення коефіцієнта \(k\).
З формули лінійної функції \(y = kx\) отримаємо, що .
З формули лінійної функції \(y = kx\) отримаємо, що .
Тому для визначення коефіцієнта \(k\) досить узяти будь-яку точку на прямій і знайти відношення ординати цієї точки до її абсциси.
Пряма проходить через точку \(M (4; 2)\), а для цієї точки маємо . Отже, \(k = 0,5\) і дана пряма є графіком лінійної функції \(y = 0,5 x\).
Графік лінійної функції \(y = kx\) будують так: беруть точку \((1; k)\) (якщо \(x = 1\), то з рівності \(y = kx\) знаходять, що \(y = k\)) і проводять пряму через цю точку і початок координат.
Іноді замість точки \((1; k)\) можна взяти іншу точку, більш зручну.
Іноді замість точки \((1; k)\) можна взяти іншу точку, більш зручну.
Від коефіцієнта \(k\) залежить кут, який побудована пряма утворює з додатним напрямком осі \(x\).
Якщо \(k> 0\), тоді цей кут гострий (як на рисунку вище), а
якщо \(k <0\), тоді цей кут тупий (як на наступному рисунку)
якщо \(k <0\), тоді цей кут тупий (як на наступному рисунку)
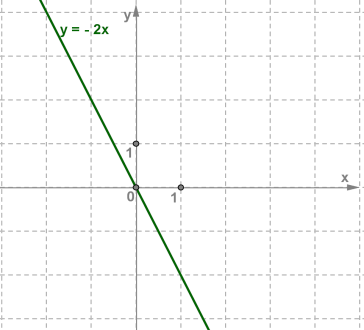
Тому коефіцієнт \(k\) у записі \(y = kx\) називають кутовим коефіцієнтом.
Узагальнюючи відомості про лінійні функції, можна зробити висновок:
Пряма, що служить графіком лінійної функції \(y=kx + b\), паралельна прямій, що служить графіком лінійної функції \(y=kx\).
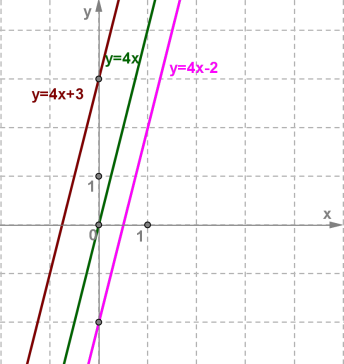
На рисунку показано паралельні прямі з одним і тим самим кутовим коефіцієнтом \(k = 4\).
Отже, коефіцієнт \(k\) у записі \(y = kx + b\) також називають кутовим коефіцієнтом, і якщо \(k> 0\), тоді пряма \(y = kx + b\) утворює з додатним напрямком осі \(x\) гострий кут, якщо \(k <0\), тоді цей кут тупий.
