Математична модель — це спосіб опису реальної життєвої ситуації (завдання) за допомогою математичної мови.
У \(7А\) вчаться \(15\) дівчаток і \(13\) хлопчиків,
у \(7Б\) вчаться \(12\) дівчаток і \(12\) хлопчиків,
у \(7В\) вчаться \(9\) дівчаток і \(18\) хлопчиків.
Відповідаючи на питання, скільки учнів у кожному із сьомих класів, доведеться тричі здійснювати одну й ту саму операцію додавання:
у \(7А\) учнів;
у \(7Б\) учні;
у \(7В\) учнів.
Використовуючи математичну мову, можна всі ці три різні ситуації об'єднати: у класі вчаться \(a\) дівчаток і \(b\) хлопчиків. Значить, усього учнів \(a + b.\)
Така математична модель даної реальної ситуації.
Така математична модель даної реальної ситуації.
У наступній таблиці наведено різні реальні ситуації та їх математичні моделі; при цьому \(a\) — число дівчаток у класі, \(b\) — число хлопчиків у тому ж класі.
| № | Реальна ситуація | Математична модель |
| 1 | У класі дівчаток і хлопчиків порівну (як у \(7Б\)) |
\(a = b\)
|
| 2 | Дівчаток на \(2\) більше, ніж хлопчиків (як у \(7А\)) |
\(a – b = 2\)
чи \(a = b + 2\) чи \(a – 2 = b\) |
| 3 | Дівчаток на \(9\) менше, ніж хлопчиків (як у \(7В\)) |
\(b – a = 9\)
чи \(b = a + 9\) чи \(a = b - 9\) |
Навіщо потрібна математична модель реальної ситуації, що вона дає, окрім короткого виразного запису?
Щоб відповісти на це питання, розв'яжемо таку задачу.
Щоб відповісти на це питання, розв'яжемо таку задачу.
Приклад:
У класі дівчаток удвічі більше, ніж хлопчиків. Якщо з цього класу підуть три дівчинки та прийдуть три хлопчики, то дівчаток буде на \(4\) більше, ніж хлопчиків. Скільки учнів у даному класі?
Розв'язання:
Нехай \(x\) — число хлопчиків у класі, тоді \(2x\) — число дівчаток. Якщо підуть три дівчинки, то залишиться \((2x-3)\) дівчаток. Якщо прийдуть три хлопчика, то стане \((x +3)\) хлопчиків. За умовою, дівчаток буде тоді на \(4\) більше, ніж хлопчиків; математичною мовою це записується так:
Нехай \(x\) — число хлопчиків у класі, тоді \(2x\) — число дівчаток. Якщо підуть три дівчинки, то залишиться \((2x-3)\) дівчаток. Якщо прийдуть три хлопчика, то стане \((x +3)\) хлопчиків. За умовою, дівчаток буде тоді на \(4\) більше, ніж хлопчиків; математичною мовою це записується так:
\(.\)
Це рівняння — математична модель задачі. Використовуючи відомі правила розв'язання рівнянь, послідовно отримуємо:
Тепер ми можемо відповісти на питання задачі: у класі \(10\) хлопчиків, а значить, \(20\) дівчаток, оскільки їх було вдвічі більше.
Відповідь: у класі всього \(30\) учнів.
Перший етап. Складання математичної моделі.
Було введено змінну \(x\) і текст завдання перекладено математичною мовою, тобто було складено математичну модель задачі у вигляді рівняння \(.\)
Було введено змінну \(x\) і текст завдання перекладено математичною мовою, тобто було складено математичну модель задачі у вигляді рівняння \(.\)
Другий етап. Робота з математичною моделлю.
Тут було розв'язано рівняння до простої відповіді \(x=10.\)
Тут було розв'язано рівняння до простої відповіді \(x=10.\)
Третій етап. Відповідь на питання завдання.
Використовуючи отриманий на другому етапі розв'язання, відповіли на питання задачі.
Використовуючи отриманий на другому етапі розв'язання, відповіли на питання задачі.
Розглянуту в прикладі математичну модель називають алгебраїчною моделлю.
Приклад:
Побудувати графік температури повітря, якщо відомо, що температуру вимірювали протягом доби і за результатами вимірювань склали таку таблицю:
| Час доби, год | \(0\) | \(2\) | \(4\) | \(6\) | \(8\) | \(10\) | \(11\) | \(14\) | \(16\) | \(18\) | \(22\) | \(24\) |
| Температура, °C | \(5\) | \(0\) | \(0\) | \(-3\) | \(-4\) | \(-2\) | \(0\) | \(6\) | \(8\) | \(5\) | \(3\) | \(3\) |
Розв'язання:
Побудуємо прямокутну систему координат. По горизонтальній осі (вісь абсцис) будемо відкладати значення часу, а по вертикальній осі (вісь ординат) — значення температури. Побудуємо на координатній площині точки, координатами яких є відповідні числа з таблиці. Усього виходить \(12\) точок.
Побудуємо прямокутну систему координат. По горизонтальній осі (вісь абсцис) будемо відкладати значення часу, а по вертикальній осі (вісь ординат) — значення температури. Побудуємо на координатній площині точки, координатами яких є відповідні числа з таблиці. Усього виходить \(12\) точок.

Поєднавши їх плавною лінією, отримаємо один з можливих графіків температури.
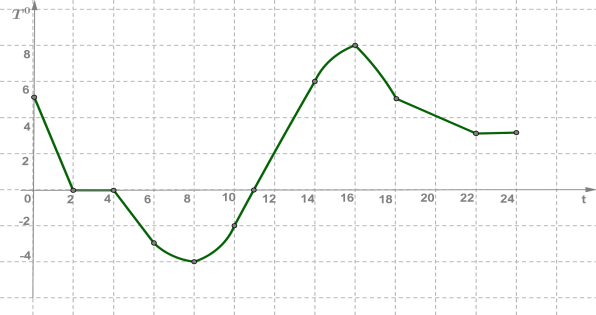
Побудований графік є математичною моделлю, що описує залежність температури від часу. Аналізуючи цей графік, можна описати словами, що відбувалося з температурою повітря протягом доби.
Розглянуту в прикладі математичну модель називають графічною моделлю.
Отже, математичні моделі бувають:
\(1)\)словесні — реальні ситуації описують словами;
\(2)\)алгебраїчні — у вигляді рівностей зі змінними, у вигляді рівнянь (як у першому прикладі);
\(3)\)графічні — у вигляді графіків залежності змінних;
\(4)\)геометричні — вивчаються в курсі геометрії.
\(1)\)словесні — реальні ситуації описують словами;
\(2)\)алгебраїчні — у вигляді рівностей зі змінними, у вигляді рівнянь (як у першому прикладі);
\(3)\)графічні — у вигляді графіків залежності змінних;
\(4)\)геометричні — вивчаються в курсі геометрії.
Важливо для розв'язання задач навчитися переходити від однієї моделі до іншої. Так, у першому прикладі, від словесної моделі перейшли до алгебраїчної, а в другому прикладі — від словесної моделі перейшли до графічної.
