Вже познайомившись з поняттям математичної моделі задачі, робимо висновок, що математичну модель реального об'єкта або деякого процесу можна подати у вигляді рівняння, формули, таблиці, діаграми, геометричної фігури, пропорції тощо.
Процес утворення рівняння з деякого твердження називають моделюванням.
Моделювання задачі у формі лінійного рівняння, або рівняння, що зводиться до нього — це процес, під час якого:
\(1\). аналізують умову задачі та визначають, що буде початковими даними, кінцевими та проміжними результатами;
\(2\). уводять позначення для певних даних — змінну;
\(3\). Записують рівняння, яке пов'язує початкові дані з кінцевими результатами — математичну модель задачі, та розв'язують його;
\(4\). аналізують отримані результати та дають відповідь на питання задачі.
Приклад:
Вік трох братів \(30\), \(20\) і \(6\) років. Через скільки років вік старшого з братів дорівнюватиме сумі віку молодших разом?
Розв'язання:
Через \(x\) років старшому буде — \((30+x)\) років, середньому — \((20+x)\), найменшому ж \((6+x) \)років.
За умовою, вік старшого дорівнюватиме сумі віку молодших, маємо математичну модель задачі — рівняння:
.
Отже, через \(4\) роки старшому виповниться \(34\) роки, й вік середнього \(24\) та молодшого \(10\), задовольнятимуть умові — \(34=24+10\).
Відповідь: \(4\) роки.
Зверни увагу!
Математичне моделювання використовують як один із найзручніших та найефективніших засобів дослідження природи та навколишнього світу.
Кожний вид текстових задач має певні загальні підходи в розв'язанні.
Зверни увагу!
Мета розв'язування задач — не лише отримання відповіді, а й опанування процесом та способом її пошуку. Тому надзвичайно важливим є заключний етап роботи над задачею — аналіз, дослідження та осмислення одержаної відповіді.
Прирівнюючи два вирази зі змінними, завжди отримують рівняння. Тому значення змінних, при яких ці вирази будуть рівними, — це розв'язок рівняння.
Пригадаємо корисності для розв'язування рівнянь:
1. Добуток дорівнює нулю, коли хоча б один з множників \(0\).
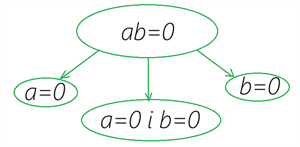
2. Інколи зручно користуватись властивістю взаємно обернених чисел, адже добуток таких чисел дорівнює \(1\).
3. Бувать випадки, коли чітко треба прийняти рішення щодо коренів рівняння. Такі випадки підпорядковуються правилу: на нуль ділити не можна, рівність "\(0x=0\)" правильна при будь-якому значенню змінної, отже маємо:
| \(0x=7\) | \(0x=0\) | \(2x=4\) |
| жодного кореня | безліч коренів | один корінь |