При діленні одночлена на одночлен:
— діляться їх коефіцієнти;
— діляться степені з однаковими основами (при діленні степенів показники віднімаються).
— діляться їх коефіцієнти;
— діляться степені з однаковими основами (при діленні степенів показники віднімаються).
Приклад:
Приклад 1.
Значення виразу дорівнює...
1) Якщо показник степеня змінної не вказаний, він дорівнює \(1\):
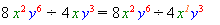
2) Ділення можна записати у вигляді звичайного дробу:
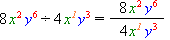
3) Діляться коефіцієнти і степені з однаковими основами:
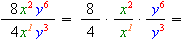
4) При діленні степенів показники віднімаються:
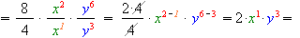
5) Члени перемножуються і дають результат:
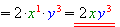
Зверни увагу!
Запам'ятай: показник степеня змінної \(1\) не записується.
Приклад:
Приклад 2.
Значення виразу дорівнює...
1) Якщо показник степеня змінної не вказаний, він дорівнює \(1\):
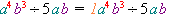 .
.2) Коефіцієнти діляться навіть тоді, коли один з них дорівнює \(1\):
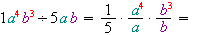 .
.3) Якщо показник степеня змінної не вказаний, він дорівнює \(1\):
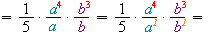 .
.4) При діленні степенів з однаковими основами показники віднімаються:
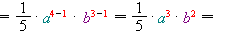 .
.5) Члени перемножуються й дають результат:
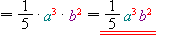 .
.Приклад:
Приклад 3.
Значення виразу дорівнює...
1) Якщо показник степеня змінної не вказаний, він дорівнює \(1\):
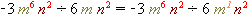 .
.2) Діляться коефіцієнти й степені з однаковими основами:
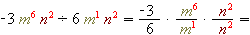 .
.3) При діленні степенів з однаковими основами показники віднімаються:
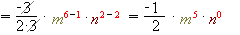 .
.4) Якщо показник степеня дорівнює \(0\), то значення степеня дорівнює \(1\), тобто, :
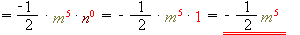 .
.