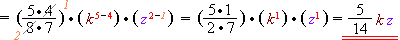При виконанні дій з дробовими одночленами здійснюються такі самі перетворення, як і при діях зі звичайними дробами.
Приклад:
Приклад \(1\).
Значення виразу дорівнює...
1) Знаменники однакові тому додаються вирази чисельників дробів:
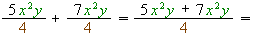 .
.2) Якщо це можливо, то скорочуються числові множники в чисельнику й знаменнику:
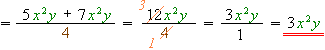 .
.Приклад 2.
Значення виразу дорівнює...
1) Дроби зводяться до спільного знаменника.
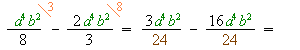 .
.2) Віднімаються значення чисельників.
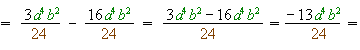 .
.3) Скоротити дріб неможливо.
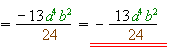 .
.Приклад 3.
Значення виразу дорівнює...
1) При множенні дробів чисельники та знаменники перемножуються між собою.
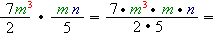
2) При множенні однакових змінних показники їх степенів додаються. Увага: якщо показник степеня не вказаний, він дорівнює \(1\).
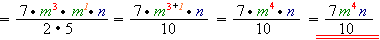
Приклад 4.
Значення виразу дорівнює...
1) При діленні одночленів коефіцієнти діляться між собою, степені з однаковими основами діляться між собою.
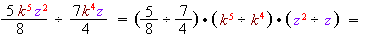
2) Ділення на дріб означає множення на обернене йому число. Увага: якщо показник степеня не вказаний, він дорівнює \(1\).
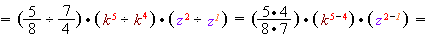
3) Якщо можливо, дріб скорочується. При діленні степенів з однаковими основами показники віднімаються.